Stabilizer Codes¶
qecc.StabilizerCode¶
Introduction¶
QuaEC includes a class, qecc.StabilizerCode, that represents error-correcting codes specified using the stabilizer formalism [Got97]. To construct a stabilizer code in QuaEC, the generators of a stabilizer group must be specified along with a particular assignment of logical operators acting on states encoded in the stabilizer code.
>>> import qecc as q
>>> stab = q.StabilizerCode(['ZZI', 'IZZ'], ['XXX'], ['ZZZ'])
>>> print stab
S = <i^0 ZZI, i^0 IZZ>
Xbars = PauliList(i^0 XXX)
Zbars = PauliList(i^0 ZZZ)
For convienence, several static methods are provided to create instances for well-known stabilizer codes.
>>> stab = q.StabilizerCode.perfect_5q_code()
>>> print stab
5-qubit perfect code
S = <i^0 XZZXI, i^0 IXZZX, i^0 XIXZZ, i^0 ZXIXZ>
Xbars = PauliList(i^0 XXXXX)
Zbars = PauliList(i^0 ZZZZZ)
Once constructed, an instance of qecc.StabilizerCode exposes properties that describe the number of physical and logical qubits, as well as the distance of the code. (Please note that calculating the distance can be extremely slow for large codes.)
>>> print (stab.nq, stab.nq_logical, stab.distance)
(5, 1, 3)
Encoders and decoders for stabilizer codes can be found in a straightforward manner using qecc.StabilizerCode.
>>> enc = stab.encoding_cliffords().next()
>>> print enc
X[0] |-> +X[0] X[1] X[2] X[3] X[4]
X[1] |-> +X[0] X[2] X[3] X[4]
X[2] |-> +X[1] X[2]
X[3] |-> +Y[0] X[1] X[3] Y[4]
X[4] |-> +X[0] X[1] Y[3] Y[4]
Z[0] |-> +Z[0] Z[1] Z[2] Z[3] Z[4]
Z[1] |-> +X[0] Z[1] Z[2] X[3]
Z[2] |-> +X[1] Z[2] Z[3] X[4]
Z[3] |-> +X[0] X[2] Z[3] Z[4]
Z[4] |-> +Z[0] X[1] X[3] Z[4]
>>> print enc.inv()
X[0] |-> -X[0] Z[3] X[4]
X[1] |-> +X[0] X[1]
X[2] |-> +X[0] X[1] X[2]
X[3] |-> -X[0] X[2] X[3] Z[4]
X[4] |-> +X[0] Y[3] Y[4]
Z[0] |-> -Z[0] Y[1] Y[3] Z[4]
Z[1] |-> -Z[0] Y[2] Z[3] Y[4]
Z[2] |-> +Z[0] Z[1] Z[2] X[3]
Z[3] |-> -Z[0] Y[1] Z[3] Y[4]
Z[4] |-> -Z[0] Z[1] X[2] Z[3] Z[4]
Stabilizer codes may be combined by the tensor product (reprsented in QuaEC by &), or by concatenation:
>>> print stab & stab
S = <i^0 XZZXIIIIII, i^0 IXZZXIIIII, i^0 XIXZZIIIII, i^0 ZXIXZIIIII, i^0 IIIIIXZZXI, i^0 IIIIIIXZZX, i^0 IIIIIXIXZZ, i^0 IIIIIZXIXZ>
Xbars = PauliList(i^0 XXXXXIIIII, i^0 IIIIIXXXXX)
Zbars = PauliList(i^0 ZZZZZIIIII, i^0 IIIIIZZZZZ)
>>> print q.StabilizerCode.bit_flip_code(1).concatenate(q.StabilizerCode.phase_flip_code(1))
S = <i^0 Z[0] Z[1], i^0 Z[1] Z[2], i^0 Z[3] Z[4], i^0 Z[4] Z[5], i^0 Z[6] Z[7], i^0 Z[7] Z[8], i^0 XXXXXXIII, i^0 IIIXXXXXX>
Xbars = PauliList(i^0 XXXXXXXXX)
Zbars = PauliList(i^0 ZZZZZZZZZ)
Class Reference¶
- class qecc.StabilizerCode(group_generators, logical_xs, logical_zs, label=None)¶
Class representing a stabilizer code specified by the generators of its stabilizer group and by representatives for the logical operators acting on the code.
Parameters: - group_generators – Generators
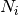 such that the stabilizer
group
such that the stabilizer
group 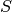 of the represented code is given by
of the represented code is given by
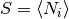 .
. - logical_xs – Representatives for the logical
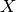 operators
acting on encoded states.
operators
acting on encoded states. - logical_zs – Representatives for the logical
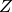 operators
acting on encoded states.
operators
acting on encoded states. - label (str) – User-facing name for the stabilizer code.
- nq¶
The number of physical qubits into which this code encodes.
- n_constraints¶
The number of stabilizer constraints on valid codewords.
- nq_logical¶
The number of logical qubits admitted by this code.
- logical_ys¶
Derives logical
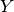 operators, given logical
operators, given logical 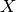 and
and 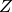 operators.
operators.
- logical_ops¶
Returns a list of all logical operators for a code in the form [Xs, Ys, Zs].
- distance¶
The distance of this code, defined by
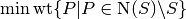 , where
, where 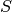 is the stabilizer group
for this code.
is the stabilizer group
for this code.Warning: this property is currently very slow to compute.
- n_correctable¶
The number of errors
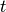 correctable by this code, defined by
correctable by this code, defined by
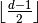 , where
, where 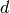 is
the distance of the code, given by the distance property.
is
the distance of the code, given by the distance property.
- stabilizer_group(coset_rep=None)¶
Iterator onto all elements of the stabilizer group
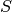 describing
this code, or onto a coset
describing
this code, or onto a coset 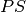 of the stabilizer group.
of the stabilizer group.Parameters: coset_rep (qecc.Pauli) – A Pauli operator 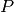 , so that the
iterated coset is
, so that the
iterated coset is 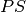 . If not specified, defaults to the
identity.
. If not specified, defaults to the
identity.Yields : All elements of the coset 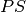 of the stabilizer
group
of the stabilizer
group 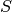 .
.
- logical_pauli_group(incl_identity=True)¶
Iterator onto the group
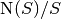 , where
, where 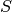 is
the stabilizer group describing this code. Each member of the group
is specified by a coset representative drawn from the respective
elements of
is
the stabilizer group describing this code. Each member of the group
is specified by a coset representative drawn from the respective
elements of 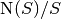 . These representatives are
chosen to be the logical
. These representatives are
chosen to be the logical 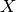 and
and 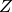 operators specified
as properties of this instance.
operators specified
as properties of this instance.Parameters: incl_identity (bool) – If False, the identity coset 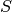 is excluded from this iterator.
is excluded from this iterator.Yields : A representative for each element of 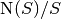 .
.
- normalizer_group(mod_s=False)¶
Returns all elements of the normalizer of the stabilizer group. If mod_s is True, returns the set
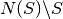 .
.
- encoding_cliffords()¶
Returns an iterator onto all Clifford operators that encode into this stabilizer code, starting from an input register such that the state to be encoded is a state of the first
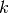 qubits, and such that the
rest of the qubits in the input register are initialized to
qubits, and such that the
rest of the qubits in the input register are initialized to
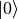 .
.Yields : instances C of qecc.Clifford such that C(q.StabilizerCode.unencoded_state(k, n - k)) equals this code.
- syndrome_to_recovery_operator(synd)¶
Returns a Pauli operator which corrects an error on the stabilizer code self, given the syndrome synd, a bitstring indicating which generators the implied error commutes with and anti-commutes with.
Parameters: synd – a string, list, tuple or other sequence type with entries consisting only of 0 or 1. This parameter will be certified before use.
- syndromes_and_recovery_operators()¶
Outputs an iterator onto tuples of syndromes and appropriate recovery operators.
- recovery_circuit_as_qcircuit(C=None, R=None)¶
Returns the recovery operator (as specified by syndromes_and_recovery_operators()), expressed as a Qcircuit array.
Parameters:
- star_decoder(for_enc=None, as_dict=False)¶
Returns a tuple of a decoding Clifford and a qecc.PauliList specifying the recovery operation to perform as a function of the result of a
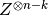 measurement on the ancilla register.
measurement on the ancilla register.For syndromes corresponding to errors of weight greater than the distance, the relevant element of the recovery list will be set to qecc.Unspecified.
Parameters: - for_enc – If not None, specifies to use a given Clifford operator as the encoder, instead of the first element yielded by encoding_cliffords().
- as_dict (bool) – If True, returns a dictionary from recovery operators to syndromes that indicate that recovery.
- minimize_distance_from(other, quiet=True)¶
Reorders the stabilizer group generators of this code to minimize the Hamming distance with the group generators of another code, using a greedy heuristic algorithm.
- stabilizer_subspace()¶
Returns a
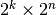 array whose rows form a basis for
the codespace of this code. Please note that by necessity, this code
is exponentially slow as a function of the numbers of physical and
logical qubits.
array whose rows form a basis for
the codespace of this code. Please note that by necessity, this code
is exponentially slow as a function of the numbers of physical and
logical qubits.
- block_logical_pauli(P)¶
Given a Pauli operator
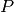 acting on
acting on 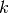 , finds a Pauli
operator
, finds a Pauli
operator 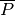 on
on 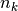 qubits that corresponds
to the logical operator acting across
qubits that corresponds
to the logical operator acting across 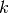 blocks of this code.
blocks of this code.Note that this method is only supported for single logical qubit codes.
- measure_gen_onto_ancilla(gen_idx)¶
Produces a circuit that measures the stabilizer code generator self.group_generators[gen_idx] onto the qubit labelled by stab.nq (that is, the next qubit not in the physical register used by the code).
Parameters: gen_idx (int) – Index of a generator of the stabilizer group, as specified by the group_generators property of this instance. Returns qecc.Circuit: A circuit that maps a measurement of group_generators[gen_idx] onto a measurement of 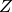 on the
ancilla qubit alone.
on the
ancilla qubit alone.
- syndrome_meas_circuit()¶
Returns a circuit which measures all stabilizer generators onto ancillae, using measure_gen_onto_ancilla.
- permute_gen_ops(perm)¶
Returns a stabilizer code with generators related to the generators of self, with every instance of {X,Y,Z} replaced with {perm[0],perm[1],perm[2]}.
Parameters: perm (list) – A list containing ‘X’,’Y’, and ‘Z’ in any order, indicating which permutation is to be applied. >>> new_stab = q.StabilizerCode.bit_flip_code(1).permute_gen_ops('ZYX') >>> assert new_stab.group_generators == q.StabilizerCode.phase_flip_code(1).group_generators
- concatenate(other)¶
Returns the stabilizer for a concatenated code, given the stabilizers for two codes. At this point, it only works for two
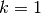 codes.
codes.
- transcoding_cliffords(other)¶
Returns an iterator onto all qecc.Clifford objects which take states specified by self, and return states specified by other.
Parameters: other – qecc.StabilizerCode
- min_len_transcoding_clifford(other)¶
Searches the iterator provided by transcoding_cliffords for the shortest circuit decomposition.
- static ancilla_register(nq=1)¶
Creates an instance of qecc.StabilizerCode representing an ancilla register of nq qubits, initialized in the state
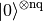 .
.Return type: qecc.StabilizerCode
- static unencoded_state(nq_logical=1, nq_ancilla=0)¶
Creates an instance of qecc.StabilizerCode representing an unencoded register of nq_logical qubits tensored with an ancilla register of nq_ancilla qubits.
Parameters: nq_logical (int) – Number of qubits to Return type: qecc.StabilizerCode
- static flip_code(n_correctable, stab_kind='Z')¶
Creates an instance of qecc.StabilizerCode representing a code that protects against weight-n_correctable flip errors of a single kind.
This method generalizes the bit-flip and phase-flip codes, corresponding to stab_kind=qecc.Z and stab_kind=qecc.X, respectively.
Parameters: - n_correctable (int) – Maximum weight of the errors that can be corrected by this code.
- stab_kind (qecc.Pauli) – Single-qubit Pauli operator specifying which kind of operators to use for the new stabilizer code.
Return type: qecc.StabilizerCode
- static bit_flip_code(n_correctable)¶
Creates an instance of qecc.StabilizerCode representing a code that protects against weight-n_correctable bit-flip errors.
Parameters: n_correctable (int) – Maximum weight of the bit-flip errors that can be corrected by this code. Return type: qecc.StabilizerCode
- static phase_flip_code(n_correctable)¶
Creates an instance of qecc.StabilizerCode representing a code that protects against weight-n_correctable phase-flip errors.
Parameters: n_correctable (int) – Maximum weight of the phase-flip errors that can be corrected by this code. Return type: qecc.StabilizerCode
- static perfect_5q_code()¶
Creates an instance of qecc.StabilizerCode representing the 5-qubit perfect code.
Return type: qecc.StabilizerCode
- static steane_code()¶
Creates an instance of qecc.StabilizerCode representing the 7-qubit Steane code.
Return type: qecc.StabilizerCode
- static shor_code()¶
Creates an instance of qecc.StabilizerCode representing the 9-qubit Shor code.
Return type: qecc.StabilizerCode
- static css_code(C1, C2)¶
Not yet implemented.
- static reed_muller_code(r, t)¶
Not yet implemented.
- static reed_solomon_code(r, t)¶
Not yet implemented.
- group_generators – Generators