Practical Bayesian Tomography
Cassandra E. Granade
Centre for Engineered Quantum Systems
joint work with Joshua Combes and D. G. Cory • arXiv coming soon
https://www.cgranade.com/research/talks/iqc/09-2015/
$
\newcommand{\ee}{\mathrm{e}}
\newcommand{\ii}{\mathrm{i}}
\newcommand{\dd}{\mathrm{d}}
\newcommand{\id}{𝟙}
\newcommand{\TT}{\mathrm{T}}
\newcommand{\defeq}{\mathrel{:=}}
\newcommand{\Tr}{\operatorname{Tr}}
\newcommand{\Var}{\operatorname{Var}}
\newcommand{\Cov}{\operatorname{Cov}}
\newcommand{\rank}{\operatorname{rank}}
\newcommand{\expect}{\mathbb{E}}
\newcommand{\sket}[1]{|#1\rangle\negthinspace\rangle}
\newcommand{\sbraket}[1]{\langle\negthinspace\langle#1\rangle\negthinspace\rangle}
\newcommand{\Gini}{\operatorname{Ginibre}}
\newcommand{\supp}{\operatorname{supp}}
$
This talk can be summarized in one slide.
\begin{equation} \Pr(\text{model} | \text{data}) = \frac{\Pr(\text{data} | \text{model})}{\Pr(\text{data})} \Pr(\text{model}) \end{equation}
OK, Two Slides
Bayesian methods for experimental data processing work.
More Seriously...
Quantum tomography: Characterizing quantum states and processes from experimental data.
From a statistical perspective, this is a parameter estimation problem.
Desirata for Tomography
We want tomographic methods that: - Provide accurate estimates. - Characterize their uncertainty. - Allow inclusion of prior knowledge. - Can track changes with time. - Come with “off-the-shelf” implementations.
We get the first two for free from taking a Bayesian perspective.
Challenges for Bayesian Tomography
- What prior should we use? - How should we update estimates in time? - How can we efficiently implement Bayesian tomography?
In this talk, we will address all three challenges.
But first,
A Short Primer on Bayesian Tomography
See also: - Jones [10/fpbsfw](https://dx.doi.org/10/fpbsfw) - Blume-Kohout [10/cn772j](https://dx.doi.org/10/cn772j)
Bayesian Parameter Estimation
Suppose we want to learn $x$ from data $D$. Then \[ \Pr(x | D) = \frac{\Pr(D | x)}{\Pr(D)} \Pr(x) \] is the posterior distribution over $x$.
$\Pr(x | D)$ describes what we know about $x$.
We estimate $x$ by the expectation value \[ \hat{x} = \expect[x | D] = \int x\,\Pr(x|D)\, \dd x. \]
This estimator is optimal for the mean squared error.
We estimate our error in the same way: \begin{align*} \expect[(x - \hat{x}(D))^2 | D] & = \expect[(x - \expect[x | D])^2 | D] \\ & = \Var(x | D). \end{align*} For multiple parameters, \[ \expect[(\vec{x} - \hat{\vec{x}})^\TT (\vec{x} - \hat{\vec{x}}) | D] = \Tr(\Cov(\vec{x} | D)). \]
More generally, \[ \hat{f} = \expect[f(x) | D]. \]
$\Pr(D | x)$ is a likelihood function that specifies an experimental model.
For state tomography, our likelihood is Born's rule, \[ \Pr(E | \rho) = \Tr[E \rho], \] where $\rho$ is a state and $E$ is a measurement effect.
Thus, Bayes' rule allows us to estimate $\rho$.
Same techniques as before apply to enable learning snapshots of dynamics. Choi-Jamiołkowski isomorphism lets us rewrite process tomography as (ancilla-assisted) state tomography.
\[ \Tr[E \Lambda(\rho)] = \Tr[(\id \otimes E) J(\Lambda) (\rho^\TT \otimes \id)] = \sbraket{\rho^\TT, E | J(\Lambda)} \]
We parameterize a state $\rho$ as a real vector $\vec{x}$, \[ x_i = \sbraket{B_i | \rho} = \Tr(B_i^\dagger \rho), \] where $\{B_i\}$ is a basis of Hermitian operators.
By convention, $\Tr(B_i) = \delta_{i0} / \sqrt{D}$. E.g.:
- Pauli basis
- Gell-Mann basis
For state tomography, the BME is approximately optimal for the fidelity (Ferrie and Keung [1503.00677](https://arxiv.org/abs/1503.00677)).
The error in an observable $X$ is given by the covariance superoperator $\Sigma\rho = \Cov(\sket{\rho})$, \begin{align*} \Var(X) & = \Var_{\rho}[\langle X\rangle_{\rho}] + \langle X^2\rangle_{\expect[\rho]} - \langle X\rangle_{\expect[\rho]}^2 \\ & = \sbraket{X | \Sigma\rho | X} + \sbraket{X | X | \hat\rho} - \langle X\rangle_{\expect[\rho]}. \end{align*} (Blume-Kohout 10/cn772j)
In practice, Bayesian mean estimation is not tractable in the exact case. We thus use particle filtering to approximate.
- Huszár and Houlsby [10/s86](https://dx.doi.org/10/s86) - Ferrie [10/7nt](https://dx.doi.org/10/7nt)
Implemented by the QInfer library for Python.
Particle Filtering for Approximate Estimation
\begin{align} \Pr(\rho) & \approx \sum_{p\in\text{particles}} w_p \delta(\rho - \rho_p) \\ w_p & \mapsto w_p \times \Pr(E | \rho_p) / \mathcal{N} \end{align}
Big advantage: we only need samples from the prior!
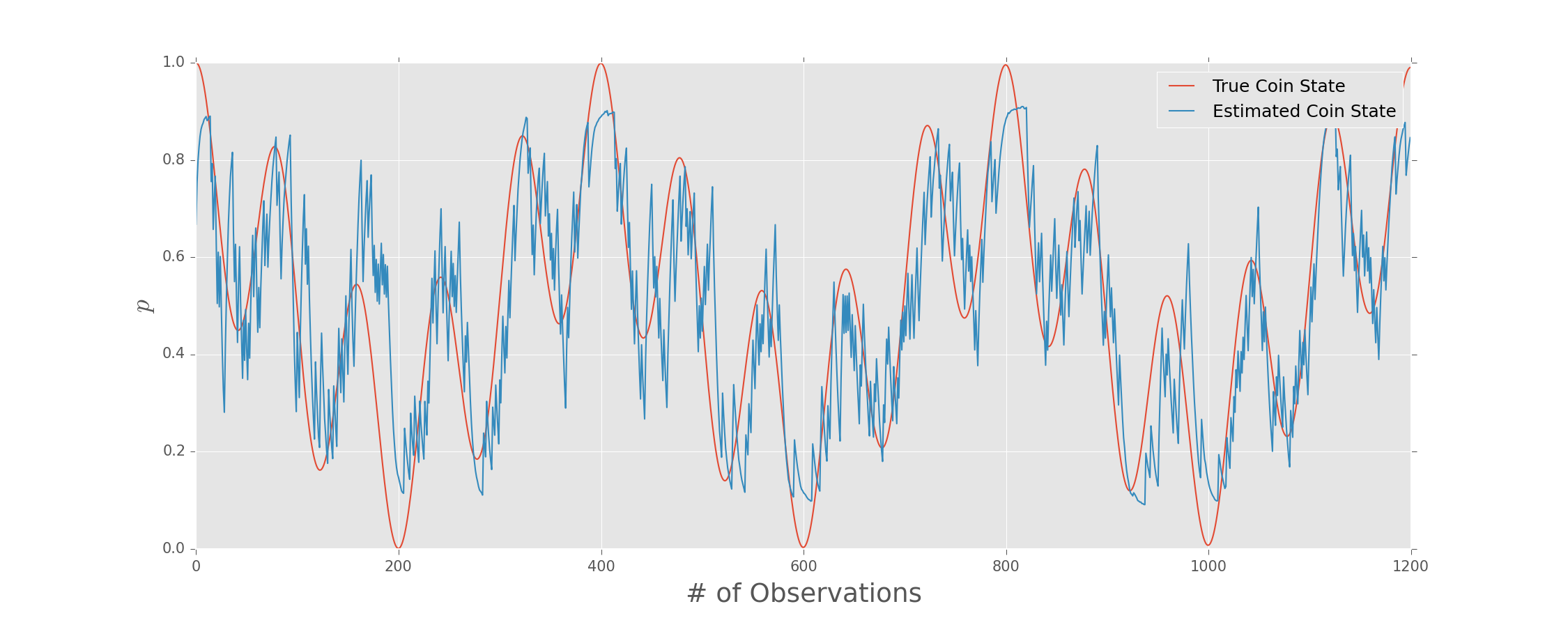
As we collect data, this becomes unstable, so we must resample.
Particle filtering is used in a range of quantum information applications.
- Hamiltonian learning: Granade *et al.* [10/s87](https://dx.doi.org/10/s87), Stenberg *et al.* [10/7nw](https://dx.doi.org/10/7nw) - Randomized benchmarking: Granade *et al.* [10/zmz](https://dx.doi.org/10/zmz) - Quantum Hamiltonian learning and bootstrapping: Wiebe *et al.* [10/tdk](https://dx.doi.org/10/tdk), Wiebe *et al.* [10/7nx](https://dx.doi.org/10/7nx) - Phase estimation: Wiebe and Granade [1508.00869](https://arxiv.org/abs/1508.00869)
Why Particle Filtering?
(You Forgot My Favorite Algorithm)
- MCMC: works, but isn't streaming or time-dependent. - Rejection filtering (Wiebe and Granade [1508.00869](https://arxiv.org/abs/1508.00869)): only keeps sufficient statistics; need more expressive instrumental distribution.
Other Advantages
Expressing as Bayesian parameter estimation / particle filtering problem affords us a few other advantages.
Region Estimation
A credible region $R_\alpha$ for $\rho$ satisfies \[ \Pr(\rho \in R_{\alpha} | D) \ge \alpha. \]
Construct from particle approximation to posterior, covariance regions (Granade *et al* [10/s87](https://dx.doi.org/10/s87)), convex hull or minimum-volume enclosing ellipse (Ferrie [10/tb4](https://dx.doi.org/10/tb4)).
Built-in to QInfer.
Model Selection
- Akaike / Bayesian information criterion: Guţă *et al.* [10/7nz](https://dx.doi.org/10/7nz), van Enk and Blume-Kohout [10/7n2](https://dx.doi.org/10/7n2) - Bayes factors: Wiebe *et al.* [10/tdk](https://dx.doi.org/10/tdk) \begin{equation} \text{BF}(A : B) = \frac{\Pr(A | \text{data})}{\Pr(B | \text{data})} \end{equation} - Model averaging: Ferrie [10/7nt](https://dx.doi.org/10/7nt)
Bayes factor–based model selection built-in to QInfer.
Hyperparameterization
\begin{align*} \text{Suppose } \vec{x} & \sim \Pr(\vec{x} | \vec{y}) \\ \text{Then, } \Pr(D | \vec{y}) & = \expect_{\vec{x} | \vec{y}} [\Pr(D | \vec{x}, \vec{y})] \\ & = \int \Pr(D | \vec{x}, \vec{y}) \Pr(\vec{x} | \vec{y})\,\dd\vec{x}. \end{align*} Marginalizing gives us a likelihood for the hyperparameters $\vec{y}$!
Allows us to include effects outside of Born's rule. For instance, non-Cauchy decoherence (Granade et al. 10/s87).
But how do we choose our prior? Let's get to the meat of things.
Informative Priors for Bayesian Tomography
In order to be useful, a prior over states should: - Have support over all states, - Allow us to encode our assumptions, and - Be efficient to draw samples from.
It helps to consider an uninformative prior first.
Ginibre Prior for Pure and Mixed States
- Let $X$ be a $N \times K$ matrix with complex Gaussian entries.
- $\rho \gets XX^\dagger / \Tr(XX^\dagger)$.
$\rank(\rho) = K$. If $K = 1$, $\rho$ is pure. If $K = N$, Hilbert-Schmidt prior.
NB: Choosing $X$ to be real gives Ginibre over redits.
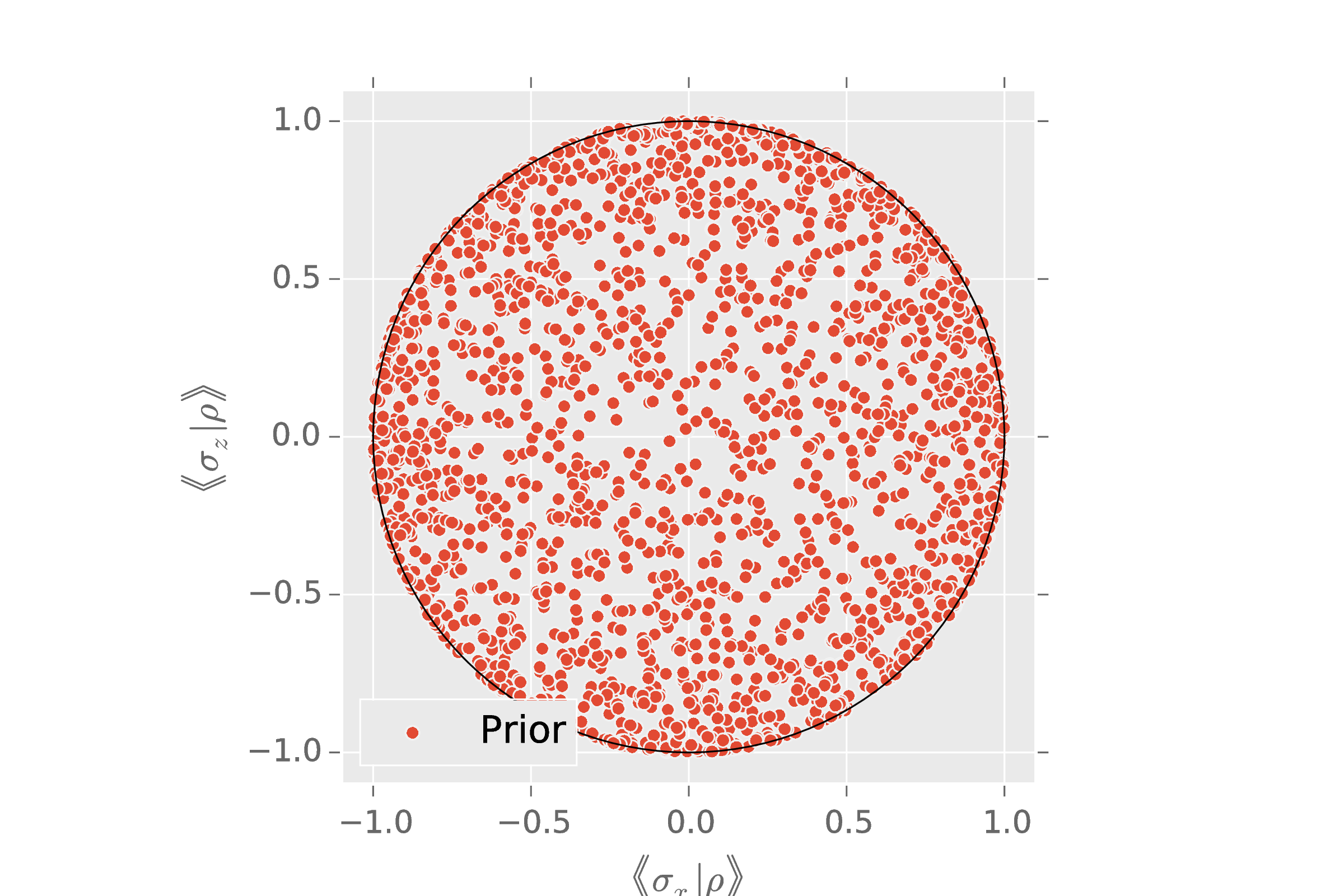
import qinfer as qi
basis = qi.tomography.pauli_basis(1)
prior = qi.tomography.GinibreReditDistribution(basis)
qi.tomography.plot_rebit_prior(prior, rebit_axes=[1, 3])
What makes $\Gini(N, K)$ uninformative? \[ \expect[\rho] = \id / N. \] The mean is the maximally-mixed state.
Other Useful Priors
- Haar, uniform over pure states - Bures, uniform over mixed states - BCSZ, uniform over CPTP maps
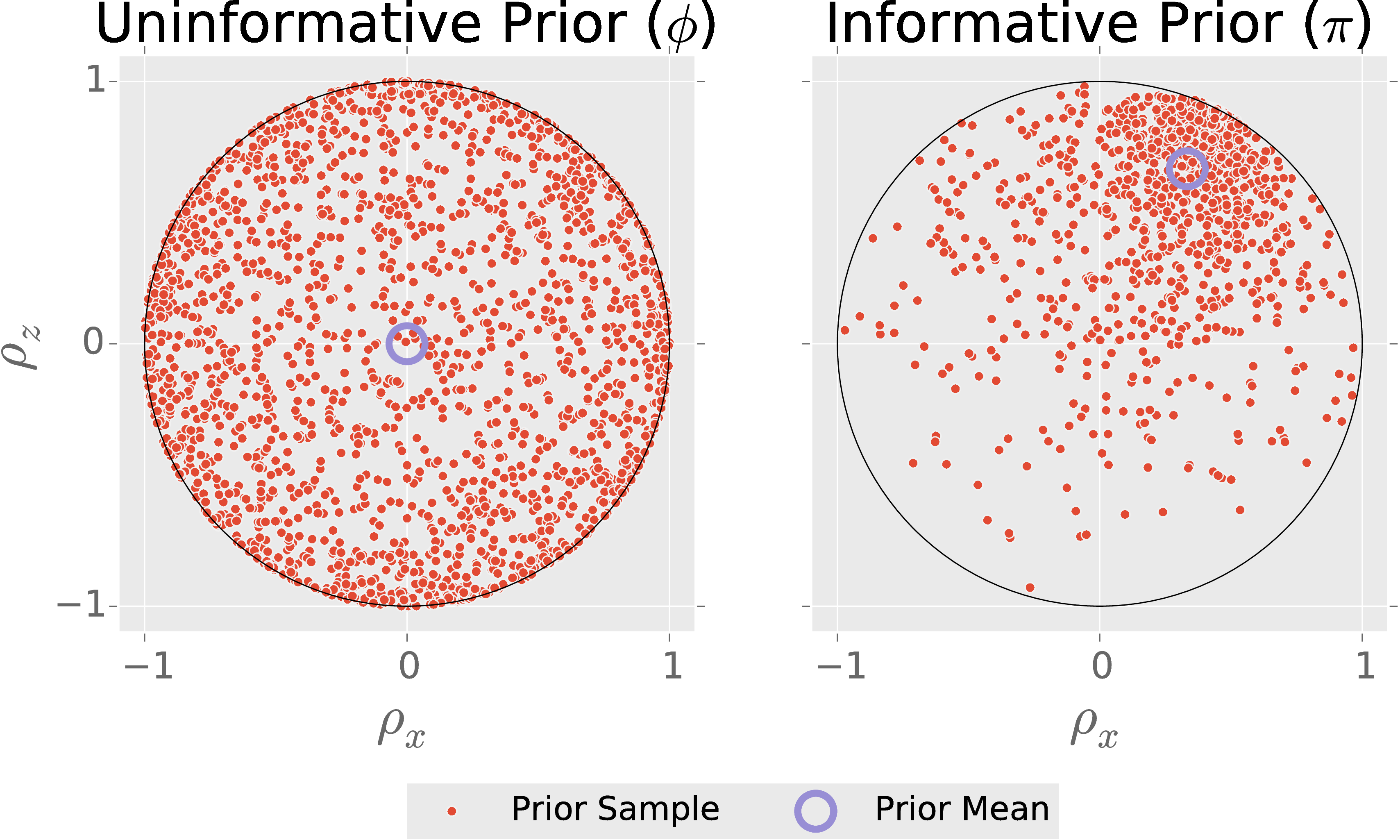
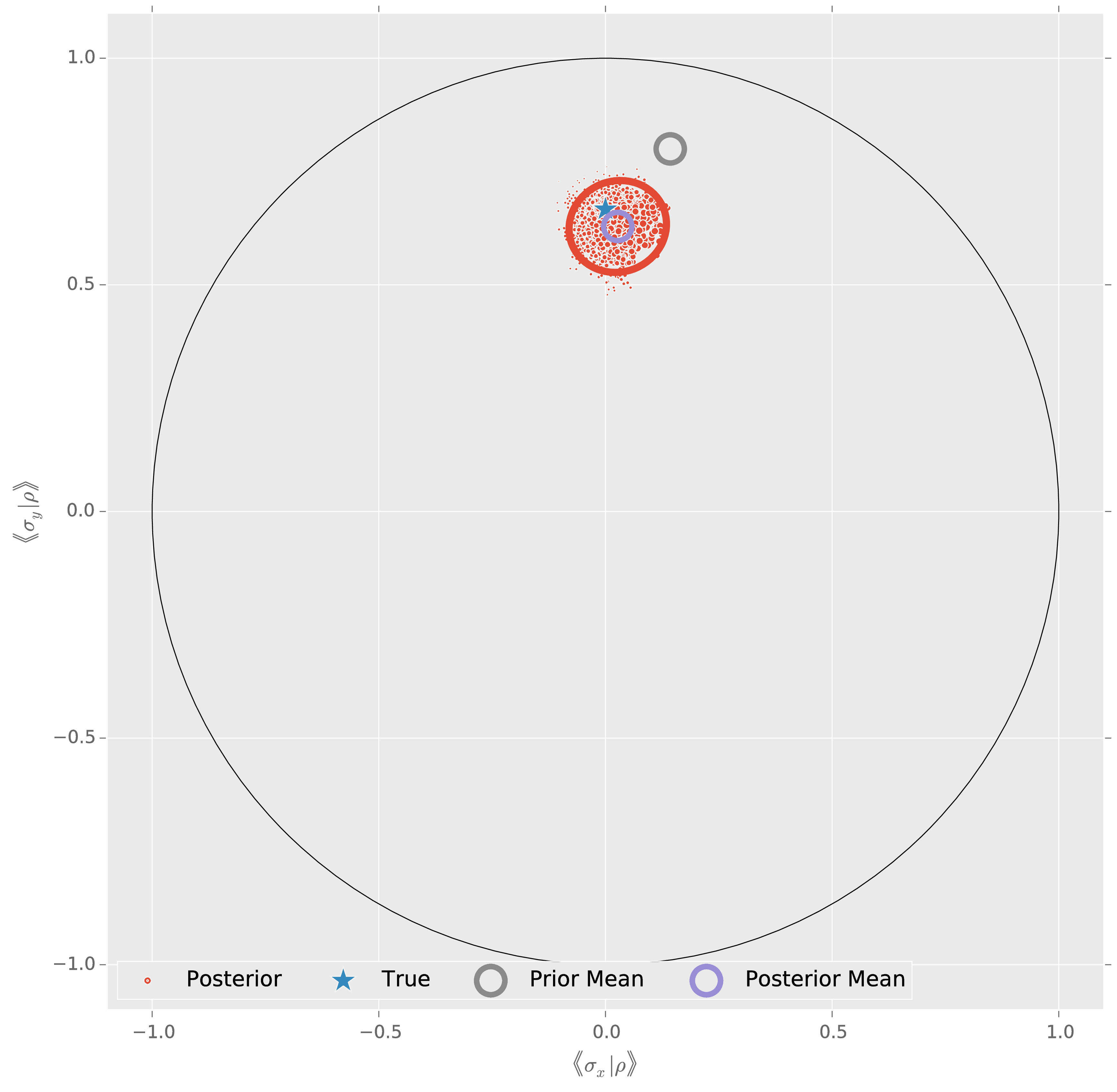
How do we add information to the prior, specifically the prior estimate state $\rho_\mu$?
Big idea: Use an ensemble of amplitude damping channels to transform a uniform prior.
Let $\phi$ be a fiducial prior. Then, for scalars $\alpha,\beta$ and a state $\rho_*$, draw $\rho_{\text{sample}}$ by:
- Draw $\rho \sim \phi$.
- Draw $\epsilon \sim \mathrm{Beta}(\alpha, \beta)$.
- $\rho_{\text{sample}} \gets (1 - \epsilon) \rho + \epsilon \rho_*$
NB: $\supp \pi \supseteq \supp \phi$
Choose $\rho_*$ s. t. $\expect_{\rho\sim\pi}[\rho] = \rho_\mu$:
\[ \rho_* = \left(\frac{\alpha + \beta}{\alpha}\right) \left( \rho_\mu - \frac{\beta}{\alpha+\beta} \frac{\id}{N} \right) \]
Choose $\alpha,\beta$ s. t. $\expect[\epsilon]$ is minimized: \[ \alpha = 1 \qquad \beta = \frac{\lambda_\min}{1 - N \lambda_\min}, \] where $\lambda_\min$ is the smallest eigenvalue of $\rho_\mu$.
That is, we contract the fiducial prior as little as possible to obtain the desired mean.
This construction preserves the support of our “flat” prior, takes $\rho_\mu$ as an input and can be easily sampled.
Inherits other assumptions by convexity (e.g.: rebit, CPTP, positivity, etc.).
Easy to Use
import qinfer as qi
import qutip as qt
I, X, Y, Z = qt.qeye(2), qt.sigmax(), qt.sigmay(), qt.sigmaz()
prior_mean = (I + (2/3) * Z + (1/3) * X) / 2
basis = qi.tomography.pauli_basis(1)
fiducial_prior = qi.tomography.GinibreReditDistribution(basis)
prior = qi.tomography.GADFLIDistribution(fiducial_prior, prior_mean)
QInfer's tomography support is backed by QuTiP.
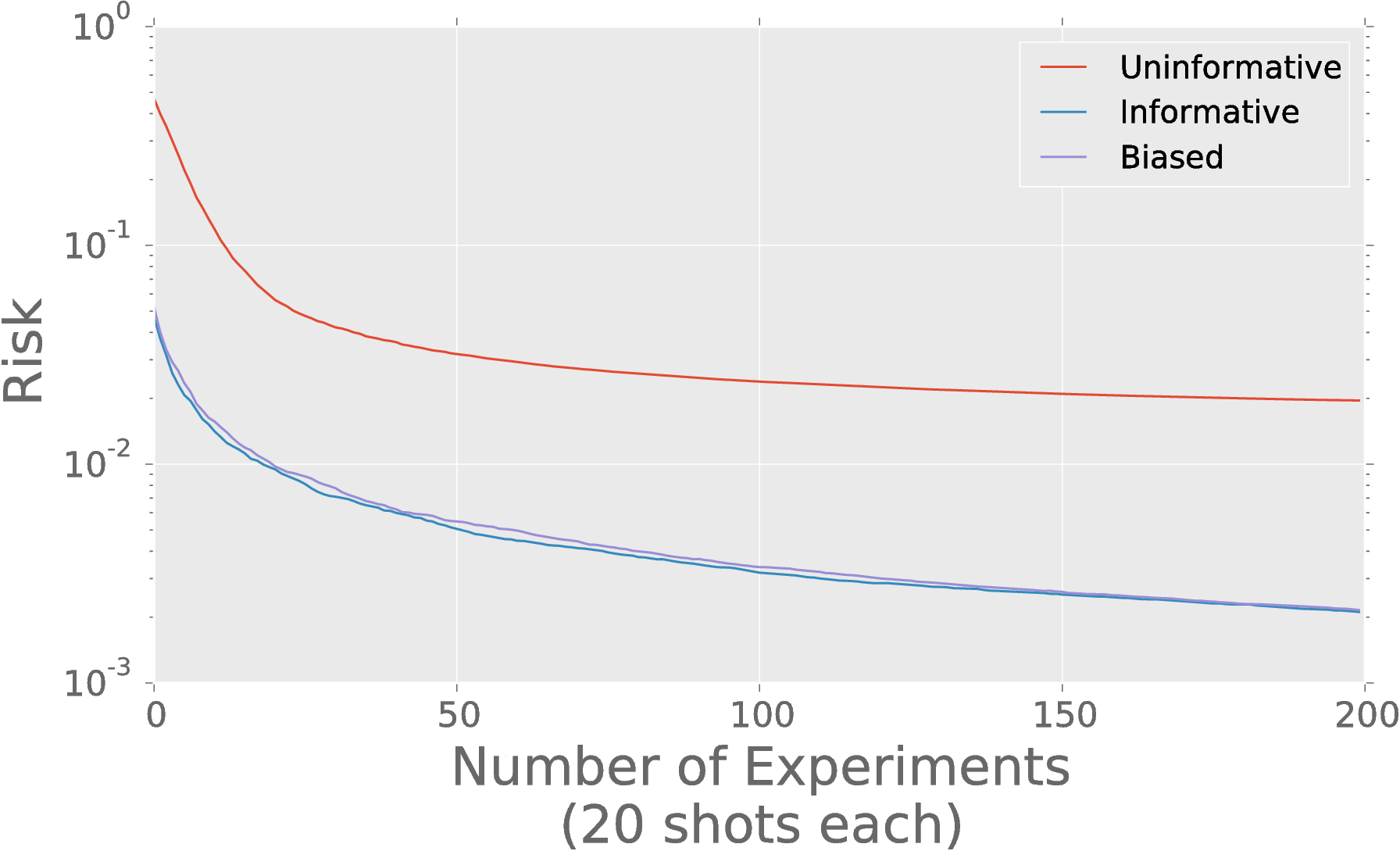
Prior Information Really Helps
Posterior covariance characterizes uncertainty.

Principal channels tell us which components dominate our uncertianty.

How Do I Use This Bloody Thing?
(a quick tutorial)
All models are wrong, some are useful. —Chris Ferrie
We've seen how to create bases and priors, to finish we need a model, an updater and a heuristic.
model = qi.BinomialModel(qi.tomography.TomographyModel(basis))
The sequential Monte Carlo updater performs Bayes updates using particle filtering.
updater = qi.smc.SMCUpdater(model, 2000, prior)
heuristic = qi.tomography.RandomPauliHeuristic(updater,
other_fields={'n_meas': 40}
)
This heuristic measures random Paulis 40 times each.
I'm Sick of This— Let's Measure!
for idx_exp in xrange(50):
experiment = heuristic()
# This is where your data goes! 💗
# For now, we'll simulate. 💔
datum = model.simulate_experiment(true_state, experiment)
updater.update(datum, experiment)
Tracking Time-Dependent States
Condensation Algorithm
Interlace Bayesian updates with diffusion \[ \rho(t_{k+1}) = \rho(t_k) + \Delta \eta. \] and truncation.
Draw each traceless parameter of the diffusion step $\Delta \eta$ from a Gaussian.
(Isard and Blake [10/cc76f6](https://dx.doi.org/10/cc76f6))
We don't need to assume that the "true" state follows a random walk.