### **Example**: Ramsey Estimation ### Suppose $H = \omega \sigma_z / 2$ for some unknown $\omega$. Traditional approach: - Prepare $\ket{+} \propto \ket{0} + \ket{1}$, measure “click” w/ pr.: $ \|\bra{+} \ee^{\ii \omega t \sigma_z / 2} \ket{+}\|^2 = \cos^2(\omega t / 2) $. - Repeat for many “shots” to estimate click pr. - Repeat for many times to estimate signal.

You'll get something that looks a bit like this:

What's $\omega$? Fourier transform and look at the peak.

We can do better.

# $H = H(\vec{x})$. # Hamiltonian learning is a special case of *parameter estimation*: given data $D$, what is $\vec{x}$?

We want an approach that can work for small and large quantum devices alike.

Punchline: our algorithm can characterize 50-qubit devices.

\begin{align} H & = \sum_{i = 1}^{50} \sum_{j = 1}^{50} \omega_{ij} \sigma_z^{(i)} \sigma_z^{(j)}, \\ \omega_{i,j} & \sim \operatorname{Uniform}\left(0, 10^{-2 (|i - j| - 1)}\right). \end{align}

To get there, we consider several different approaches to parameter estimation.

Analytic Sergeevich et al. c4vv95 Ferrie, Granade, and Cory tfx
Rejection filter Wiebe and Granade bk9d
Particle filter Doucet et al. bmch
Likelihood-free particle filter Ferrie and Granade tdj
Quantum bootstrapping Wiebe, Granade and Cory 7nx

### The Likelihood Function ### $\|\bra{+} \ee^{\ii \omega t \sigma_z / 2} \ket{+}\|^2$ defines probability $\Pr(d | \omega; t)$ for every outcome $d$, model $\omega$ and experiment $t$. Basis for both maximum-likelihood and Bayesian methods.

Aside: Why Bayesian?

Frequentist methods work. Bayesian methods also work.
Methodology should follow the question of interest.

Example

What should I believe the properties of my system are, given my experience and a set of observations?

Bayesian question, hence Bayesian answer.

### Bayesian Parameter Estimation ### The likelihood tells us what we learn from data: $$ \Pr(\vec{x} | d; e) = \frac{\Pr(d | \vec{x}; e)}{\Pr(d | e)} \Pr(\vec{x}) $$ --- Estimate $\hat{x} = \expect[\vec{x} | d; e] = \int \vec{x} \Pr(\vec{x} | d; e)\dd \vec{x}$. - **Optimal** for mean—squared error.

Inference as an Iterative Algorithm

Input: Prior $\Pr(\vec{x})$, data set $D$, likelihood $\Pr(d | \vec{x}; e)$

$p(\vec{x}) \gets \Pr(\vec{x})$
For each datum $d \in D$ and experiment $e$:
- Update based on $d$:
  $p(\vec{x}) \gets \Pr(d | \vec{x}; e) p(\vec{x}) / \Pr(d)$.
Return $\hat{x} = \int \vec{x}\,p(\vec{x})\,\dd\vec{x}$.

--- At each step, $p(\vec{x})$ also encodes our uncertainty. $ \expect[(x - \hat{x})^2 | d; e] = \mathbb{V}[x \mid d; e]. $

We can use our posteriors to make *adaptive* decisions: $$ e_* = \operatorname{arg min}_e \expect_d[\mathbb{V}(x | d; e)] $$

### **Example**: $x = (\omega)$ ### Can analytically find posterior for Gaussian priors, use to adaptively choose $t_k$. ![](./figures/how-t2.png)

**Problem**: may be intractable to analytically compute $$ \hat{x} \defeq \int \Pr(\vec{x} | d; e) \dd\vec{x} = \int \frac{ \Pr(d | \vec{x}; e) }{ \int \Pr(d | \vec{x}; e) \Pr(\vec{x}) \dd\vec{x} } \Pr(\vec{x}) \dd\vec{x}. $$

--- **Answer**: numerically approximate $\int f(\vec{x}) \Pr(\vec{x} | d)\dd\vec{x}$. *Efficient* to use Monte Carlo integration if we can sample from the posterior $\Pr(\vec{x} | d; e)$.

## Rejection Sampling ## Given samples from $\Pr(\vec{x})$ and likelihood function $\Pr(d | \vec{x}; e)$, how do we sample from posterior for datum $d$? - Draw $\vec{x} \sim \Pr(\vec{x})$, accept $\vec{x}$ w/ $\Pr(d | \vec{x}; e)$. Accepted samples are distributed according to posterior.

Rejection Sampling Isn't Enough

Let $D = {d_1, \dots, d_k}$ be a set of data.

$$ \Pr(\text{accept} | \vec{x}) = \Pr(D | \vec{x}) = \prod_{d \in D} \Pr(d | \vec{x}) \overset{k \to \infty}{\longrightarrow} 0. $$

Example: Biased Coin $x = (p)$

$\Pr(H | p) = p$, $d \in \{H, T\}$.

$p \approx 0.5 \Longrightarrow \Pr(d_1, \dots, d_k | p) \approx 1 / 2^k$.

We will accept exponentially few samples!

### Gaussian Resampling ### For each datum $d$, use rejection sampling to approximate posterior moments: - $\bar{x} \gets \expect[\vec{x} | d]$. - $\Sigma \gets \operatorname{Cov}[\vec{x} | d] = \expect[\vec{x} \vec{x}^\TT | d] - \bar{x} \bar{x}^\TT$.

--- At the next iteration, draw prior samples from Gaussian with these moments: $$ \vec{x} \mid d \sim \mathcal{N}(\bar{x}, \Sigma) $$ Keeps $\Pr(\text{accept}) \approx \text{constant}$.

Can compute $\bar{x}$, $\Sigma$ from one sample at a time by accumulating

$$ x_{\Sigma} = \sum x \text{ and } x^2_{\Sigma} = \sum x^2. $$

\begin{align} \bar{x} & = x_{\Sigma} / n_{\text{accept}} \\ \Sigma & = x^2_{\Sigma} / n_{\text{accept}} - \bar{x}^2. \end{align}

Welford's algorithm: numerically-stable modification.

Rejection Filtering (RejF)

Input: Prior mean $\bar{x}$, prior covariance $\Sigma$, number of samples $m$ to accept.

For each datum $d$ and experiment $e$:

$n, \bar{x}', M_2 \gets 0$ Initialize Welford.
While $n < m$:

Draw $\vec{x} \sim \mathcal{N}(\bar{x}, \Sigma)$. Sample f/ prior.
Accept $\vec{x}$ w/ $\Pr(d | \vec{x}; e)$.
If accepted, update $n$, $\bar{x}'$, $M_2$.

$\bar{x} \gets \bar{x}'$, $\Sigma \gets M_2 / (n - 1)$. Est. moments.

Easy to implement and embed in control hardware.

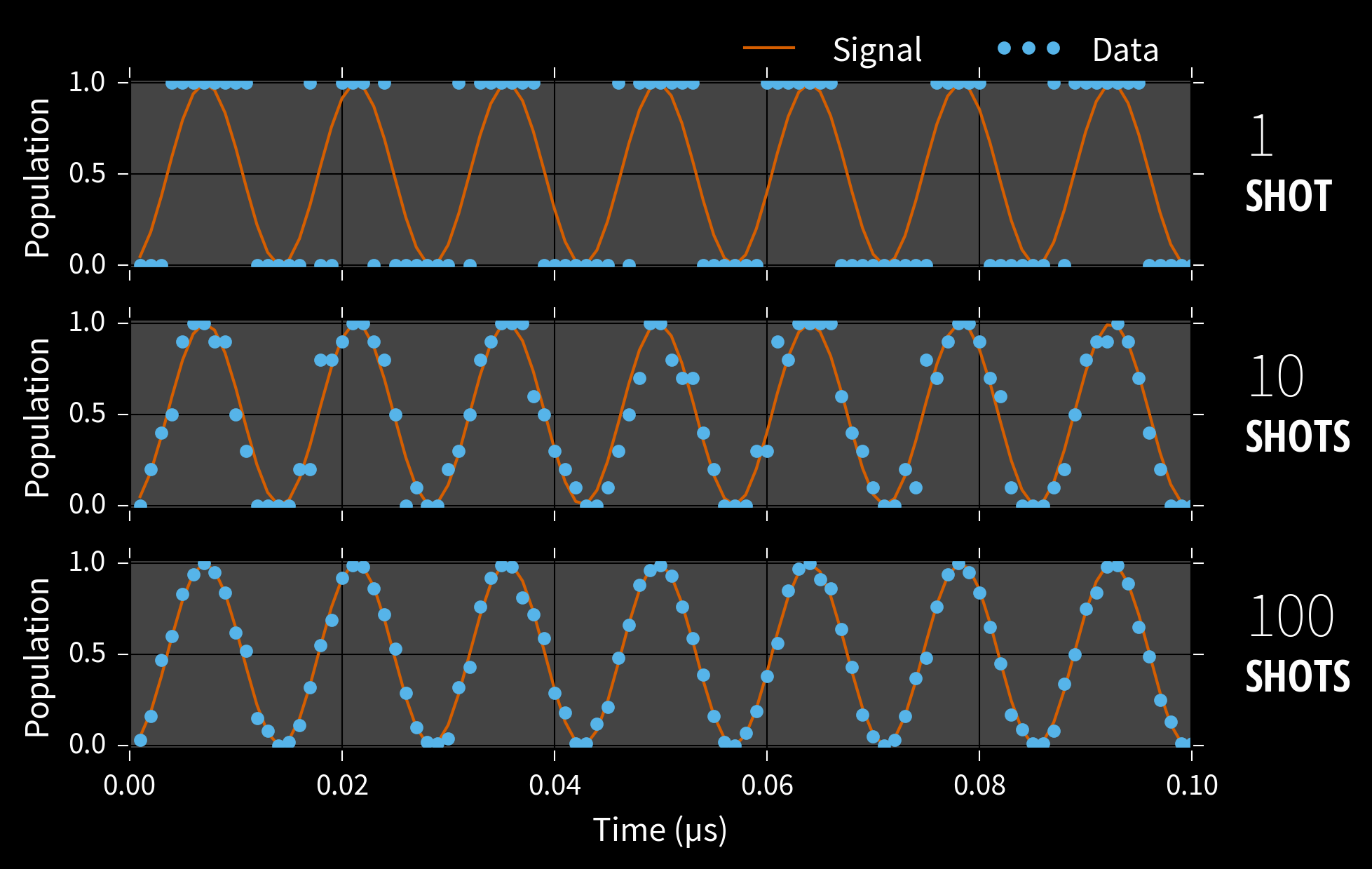
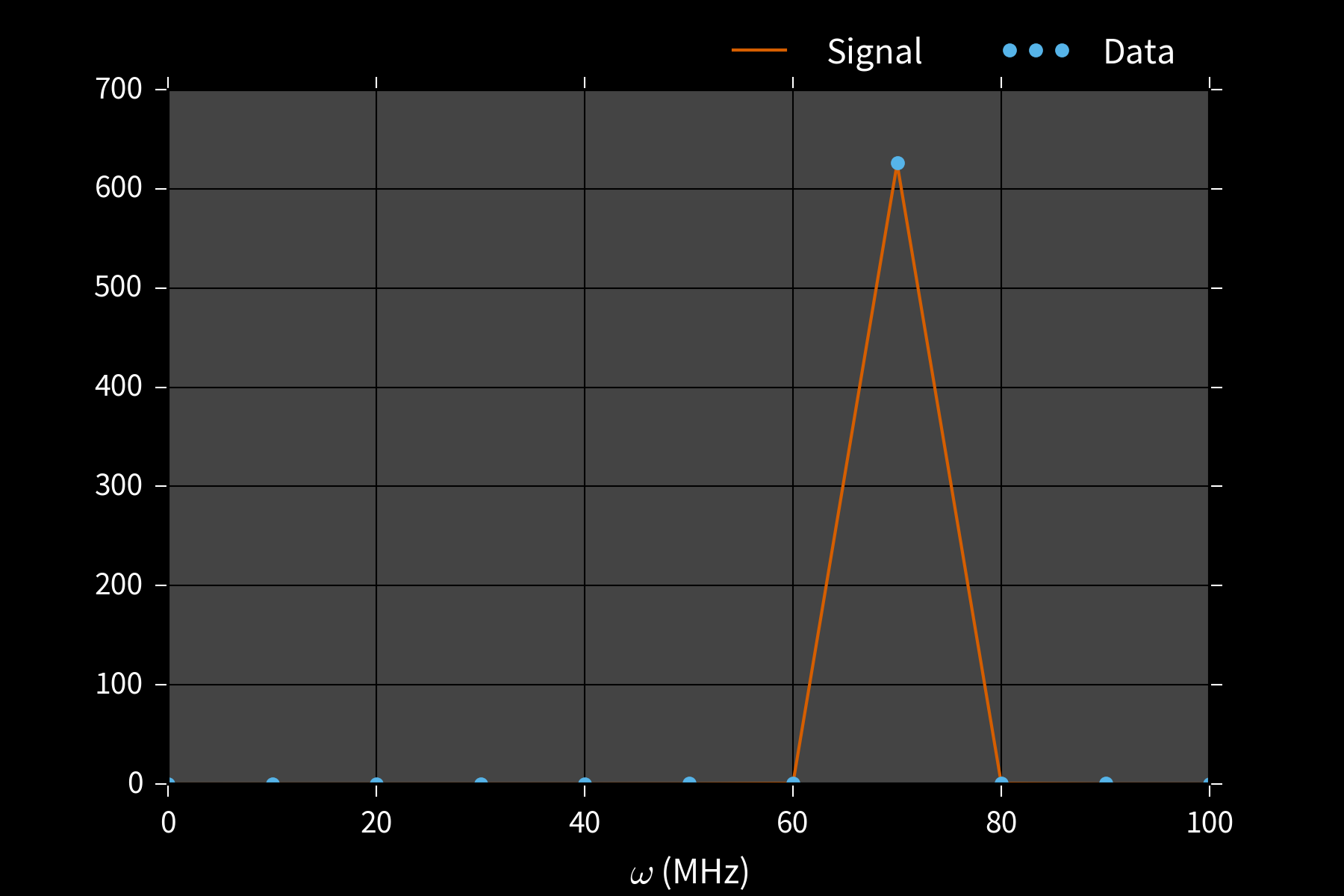
Example: Phase Estimation, $x = (\phi)$

Prepare state $\ket{\phi}$ s. t. $U\ket{\phi} = \ee^{\ii \phi}\ket{\phi}$, measure to learn $\phi$.

$\Pr(1 | \phi; M, \theta) = \cos^2(M [\phi - \theta])$

Applications
Interferometry / metrology Higgins et al. crwd6w
Gate calibration / robust PE Kimmel et al. bmrg
Quantum simulation and chemistry Reiher et al. 1605.03590

Example: Phase Estimation, $x = (\phi)$

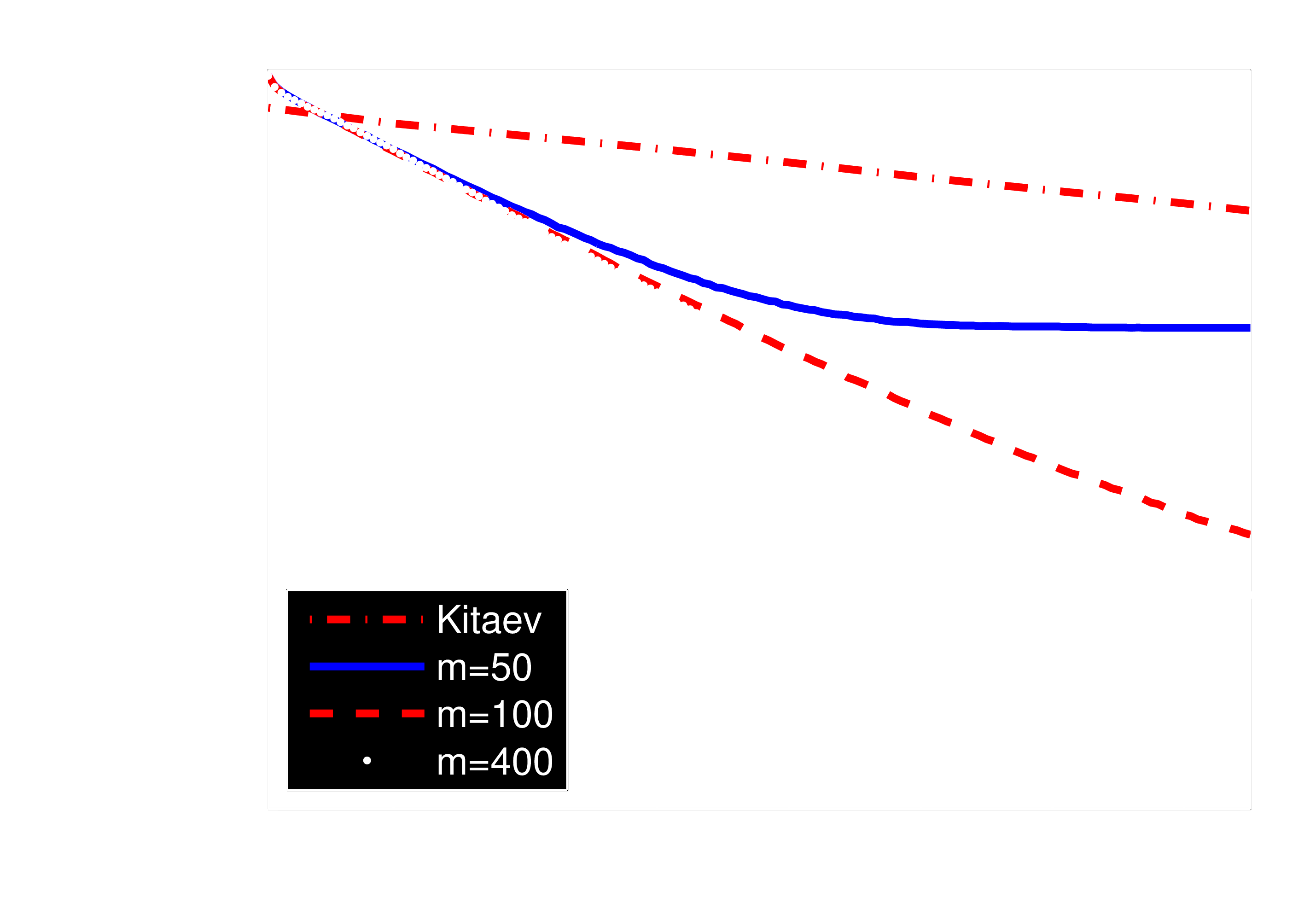
**Drawback**: RejF requires posterior after each datum to be $\approx$ Gaussian.

We can solve this by using a more general approach: - Weaken Gaussian assumption. - Generalize the rejection sampling step.

Liu-West Resampler

If we remember each sample $\vec{x}$, we can use them to relax RejF assumptions.

Input: $a, h \in [0, 1]$ s.t. $a^2 + h^2 = 1$, distribution $p(\vec{x})$.

Approximate $\bar{x} \gets \expect[\vec{x}]$, $\Sigma \gets \operatorname{Cov}(\vec{x})$
Draw parent $\vec{x}$ from $p(\vec{x})$.
Draw $\vec{\epsilon} \sim \mathcal{N}(0, \Sigma)$.
Return new sample $\vec{x}' \gets a \vec{x} + (1 - a) \bar{x} + h \vec{\epsilon}$.

### Why Does Liu-West Work? ### \begin{align} \vec{x}' & \gets a \vec{x} + (1 - a) \bar{x} + h \vec{\epsilon} \\\\ \expect[\vec{x}'] & = [a + (1 - a)] \bar{x} \\\\ \Cov(\vec{x}') & = (a^2 + h^2) \Cov(\vec{x}). \\\\ \Longrightarrow a^2 + h^2 & = 1 \text{ preserves } \expect[\vec{x}], \Cov(\vec{x}). \end{align} --- Mixes original approximation with $1 - a$ of a Gaussian matching moments. - $a \to 0$: RejF (assumed density) approx - $a \to 1$: Bootstrap - $a = 0.98$: typical case (2% Gaussian).

### From Samples to Particles ### Define a particle $(w_i, \vec{x}_i)$ as a sample $\vec{x}_i$ and a weight $w_i \in [0, 1]$. - $\expect[\vec{x}] = \sum_i w_i \vec{x}_i$ - $\Cov(\vec{x}) = \sum_i w_i \vec{x}_i \vec{x}_i^\TT - \expect[\vec{x}]\expect^\TT[\vec{x}]$ - $\expect[f(\vec{x})] = \sum_i w_i f(\vec{x}_i)$ --- Corresponds to $ p(\vec{x}) \approx \sum_i w_i \delta(\vec{x} - \vec{x}_i). $

Particles can represent distributions using either
weights or positions.

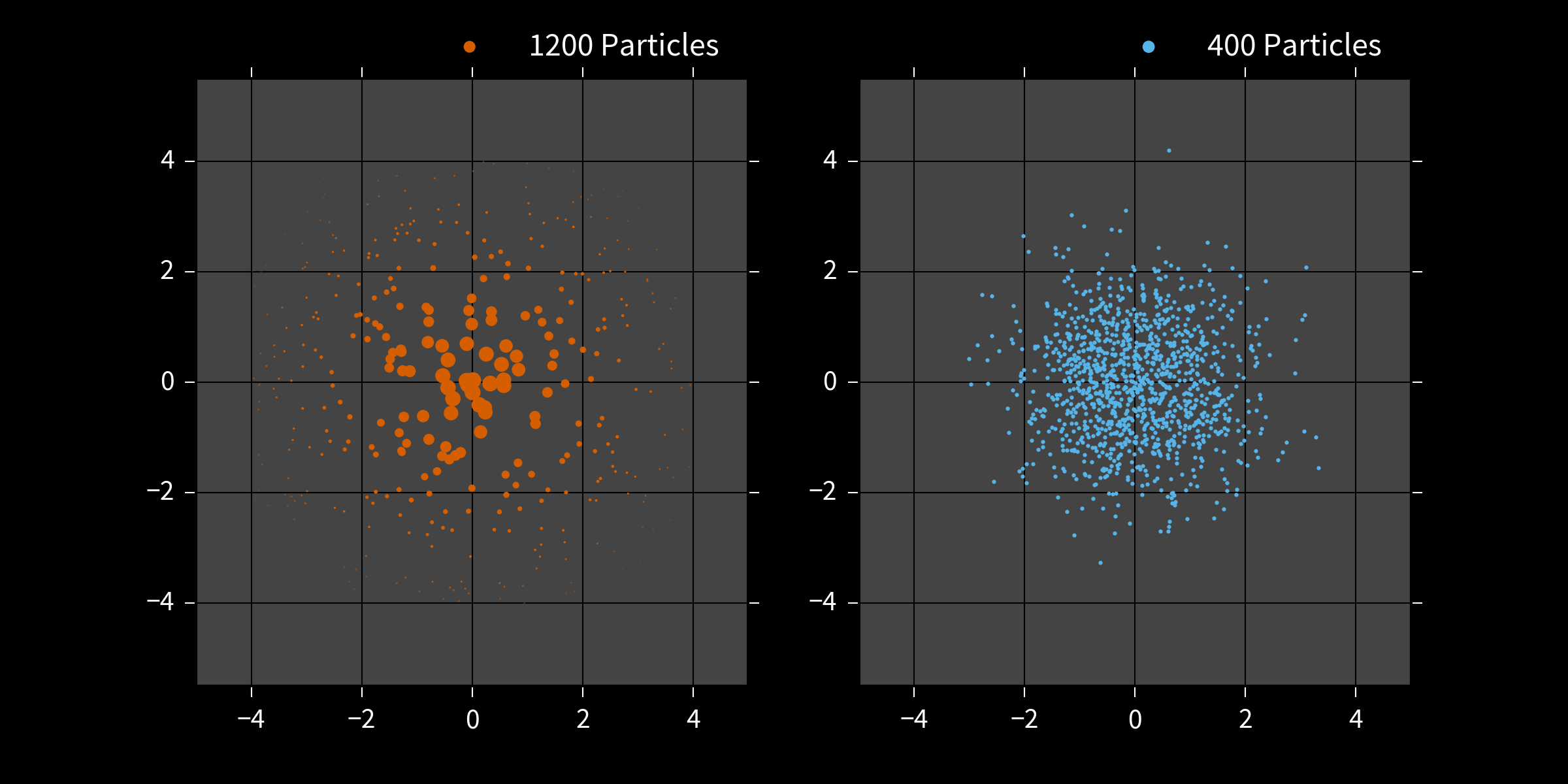
Particle Filter

Draw $N$ initial samples $\vec{x}_i$ from the prior $\Pr(\vec{x})$ w/ uniform weights.
Instead of rej. sampling, update weights by \begin{align} \tilde{w}_i & = w_i \times \Pr(d | \vec{x}_i; e) \end{align}
Renormalize. \begin{align} w_i & \mapsto \tilde{w}_i / \sum_i \tilde{w}_i \end{align}
Periodically use Liu-West to draw new $\{\vec{x}_i\}$ with uniform weights. Store posterior in positions.

Useful for Hamiltonian models...

Rabi/Ramsey/Phase est. Granade et al. s87
Swap spectroscopy Stenberg et al. 7nw

...as well as other QIP tasks.

Tomography Huszár and Holsby s86 Struchalin et al. bmg5 Ferrie 7nt Granade et al. bhdw, 1605.05039
Randomized benchmarking Granade et al. zmz
Continuous measurement Chase and Geremia chk4q7
Interferometry/metrology Granade 10012/9217

Estimation in Practice

We need a bit more to make particle filtering a practical solution.

Error bars How well do we know $\vec{x}$?
Time-dependence $\vec{x} = \vec{x}(t)$
Software impl. Off-the-shelf.

Dealing with each in turn...

Error Bars

Particle filters report credible regions $X_\alpha$ s.t. $$ \Pr(\vec{x} \in X_\alpha | d; e) \ge \alpha. $$

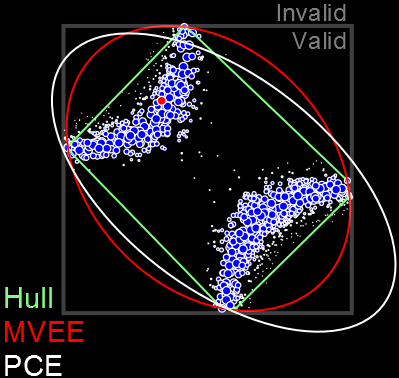
E.g.: Posterior covariance ellipse, convex hull, MVEE.

Time-Dependence

In addition to updating particle weights, move each particle stochastically:

$$ \vec{x}(t_{k+1}) = \vec{x}(t_k) + \vec{\eta},\qquad \vec{\eta} \sim \mathcal{N}(0, (t_{k+1} - t_k) \Sigma) $$

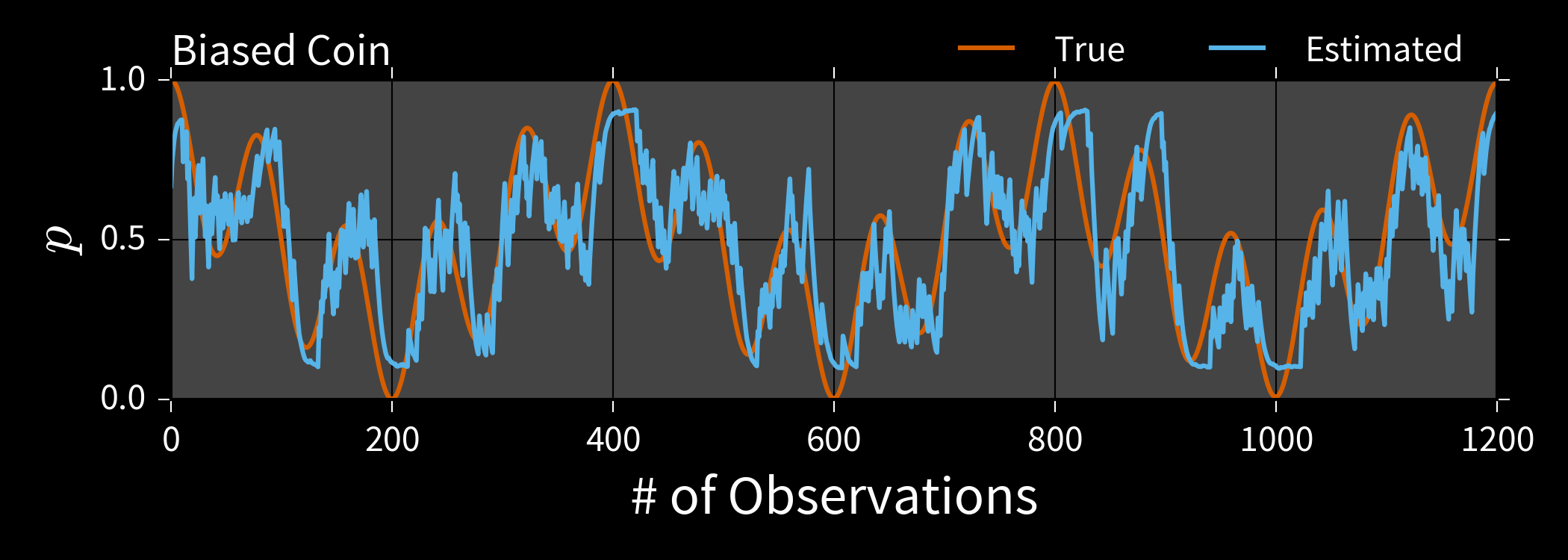
### Software Implementation ### We provide **QInfer**, an open-source implementation for use in quantum information. Written in Python, works with MATLAB and Julia.

--- Puts focus on algorithms and experiments, not implementations.

Bigger and Better

We've seen that filtering is useful for estimating small quantum models. Now let's push on to bigger systems.

What challenges do we face for large systems?

Simulation Costs

\begin{align} \tilde{w}_i & = w_i \times \color{red}{\Pr(d | \vec{x}_i; e)} \\ w_i & \mapsto \tilde{w}_i / \sum_i \tilde{w}_i \end{align}

- $\Pr(d | \vec{x}_i; e)$ is a *simulation*. - Need to simulate for each particle (~1000s calls/datum). - Infeasible for large quantum models. Let's do better: use *quantum* simulation instead.

### Two Kinds of Simulation ### ![](figures/simulators.png) Weak simulators produce *plausible datasets*.

### Likelihood-Free RejF ### Replace rej. sampling step by drawing datum from likelihood instead of computing exact value: - Draw datum $d'$ from $\Pr(d | \vec{x}; e)$. - Accept $\vec{x}$ if $d = d'$.

### Likelihood-Free Particle Filtering ### Can also use frequencies $f$ from weak simulation to approximate likelihoods in particle filtering. $$ \widehat{\Pr}(d | \vec{x}; e) = \frac{f(d | \vec{x}; e)}{k} $$ $k$: number of weak simulation calls used.

### **Example**: Noisy Coin ### How well can we learn the bias $x = (p)$ of a noisy coin? $$ \Pr(\text{click} | p) = 0.95 p + 0.1 (1 - p) $$

### Quantum Hamiltonian Learning ### We can learn large Hamiltonians by using likelihood-free filtering w/ interactivity. ![](figures/iqle.png) Perform weak simulations on trusted device only.

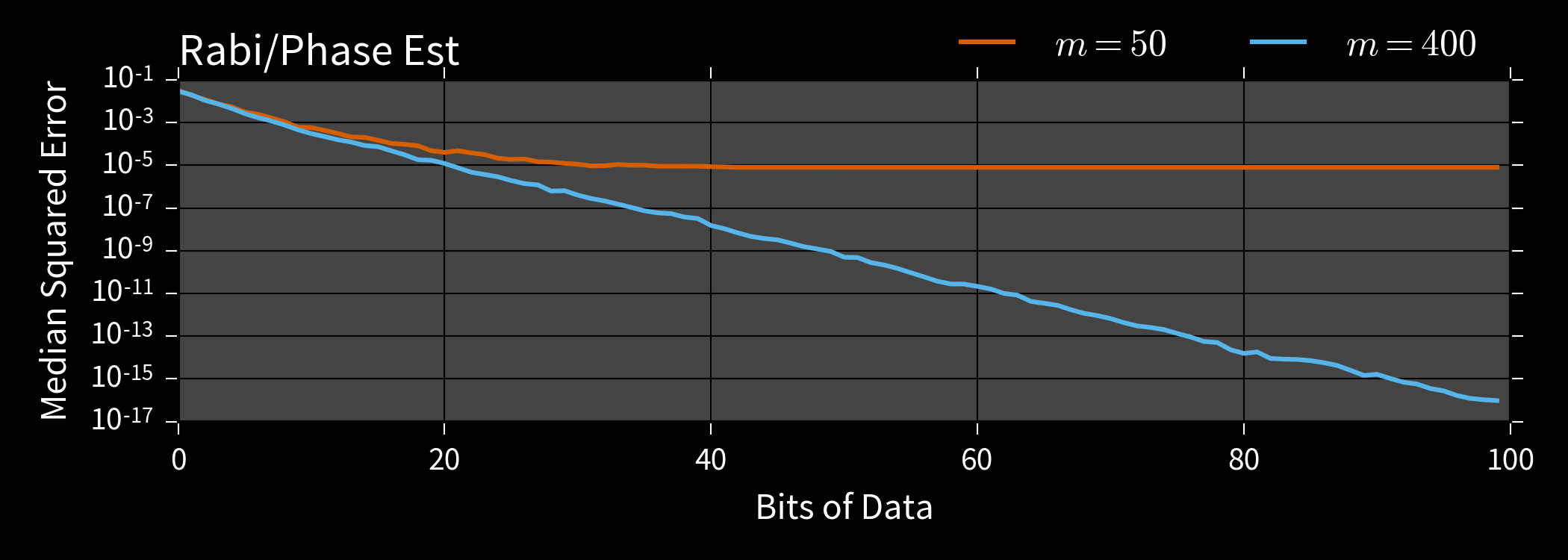
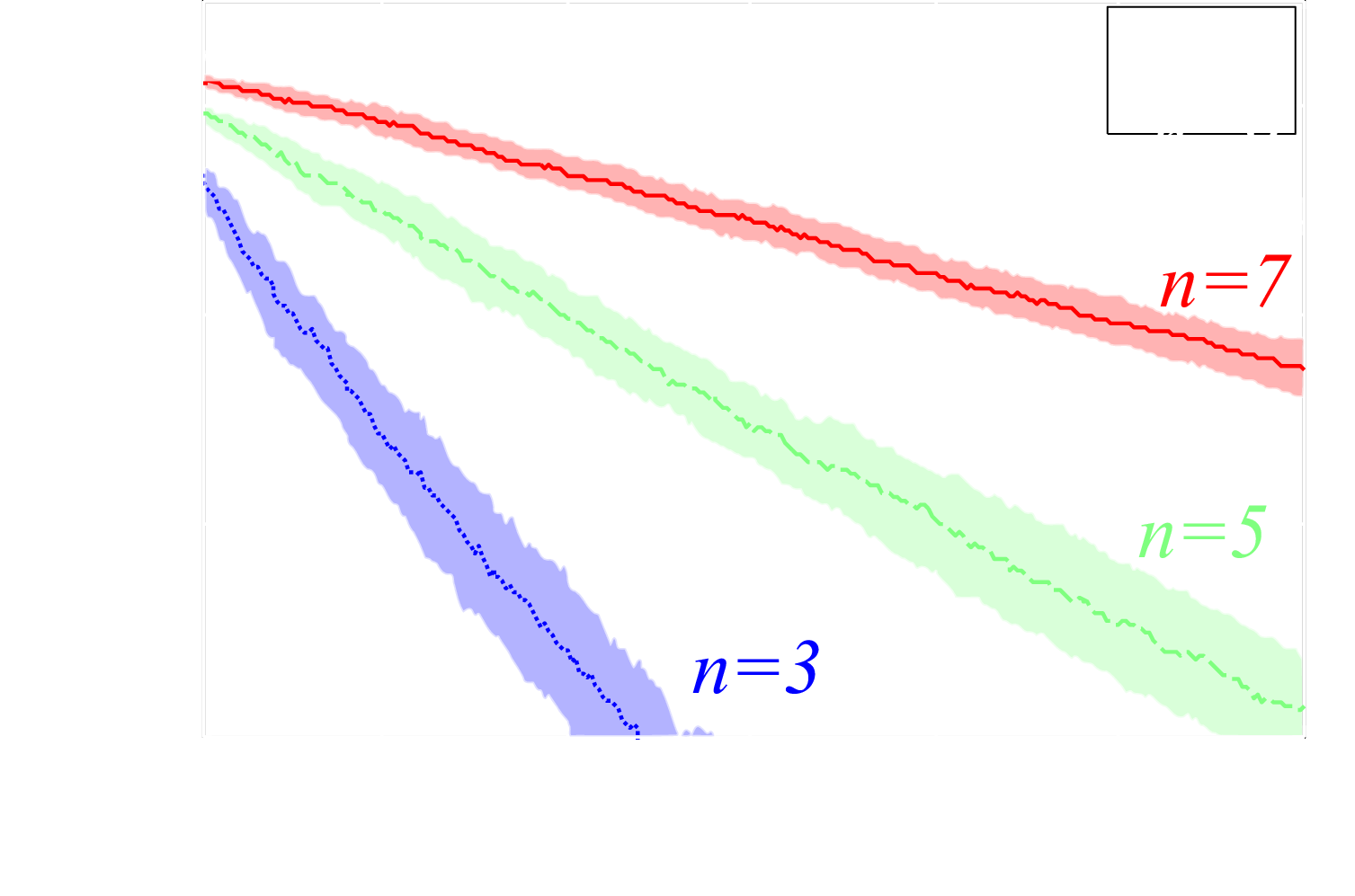
Example: Ising on Complete Graph

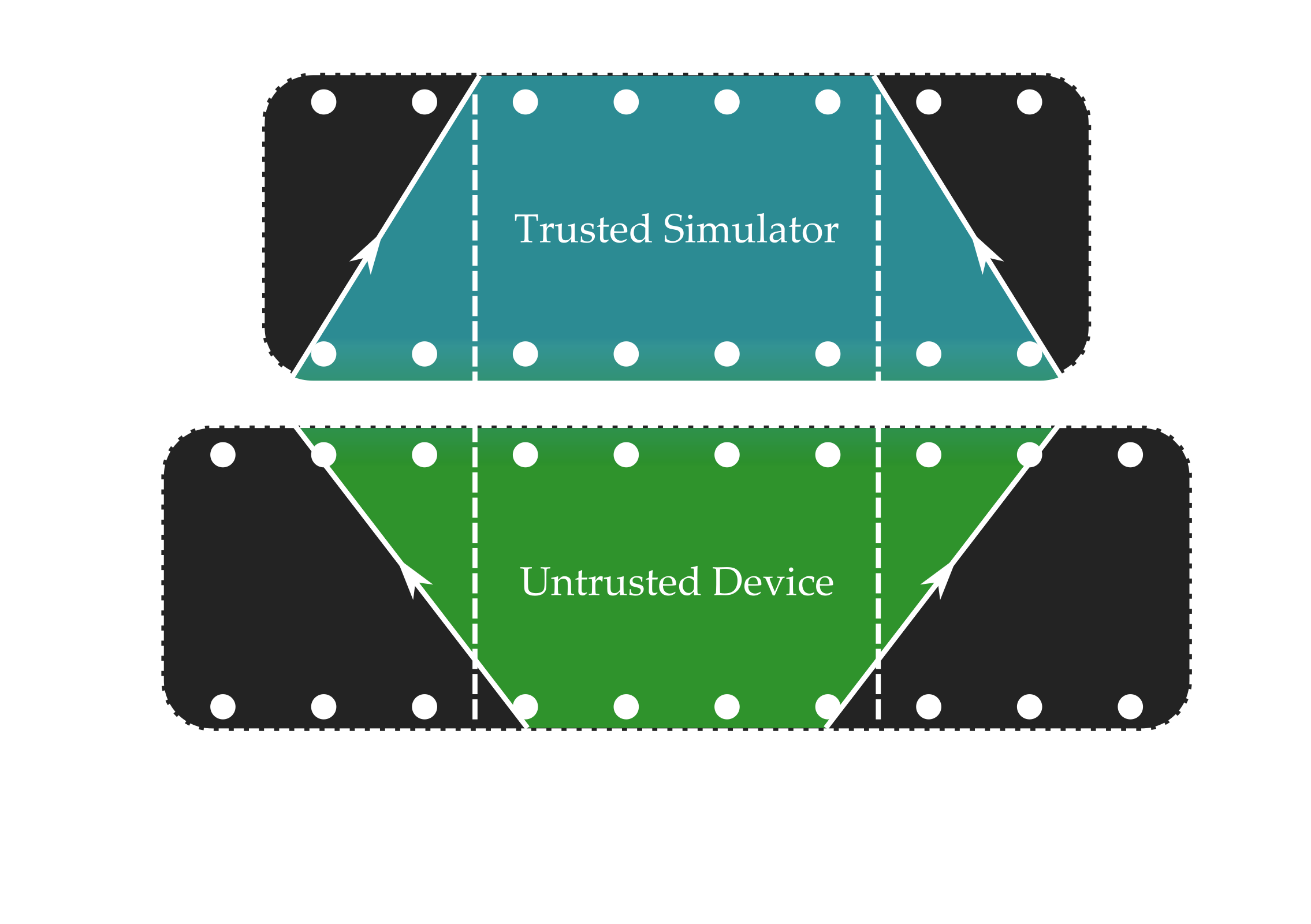
Robust even to wrong model. ($0.5$ NN + $10^{-4}$ Complete) ![](figures/qhl-bad-model.png)

Quantum Bootstrapping

One important approximation f/ physical insight:
information locality.

Allows using small trusted device to learn large Hamiltonians.

Approximation quality can be bounded if Lieb-Robinson velocity is finite.

Scan trusted device across untrusted.

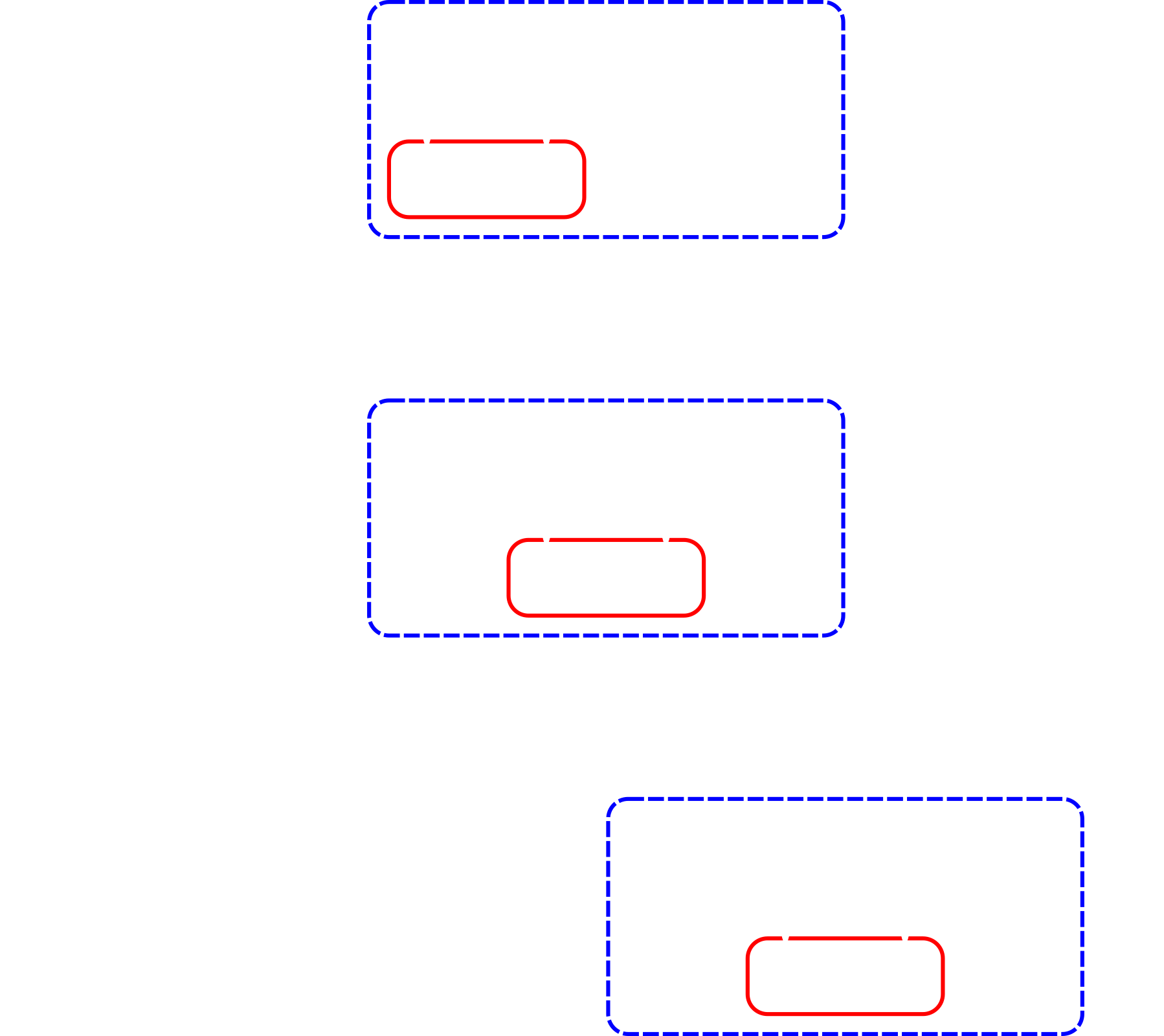
Run particle filter only on supported parameters.

50 qubit Ising chain, 8 qubit simulator, 4 qubit observable

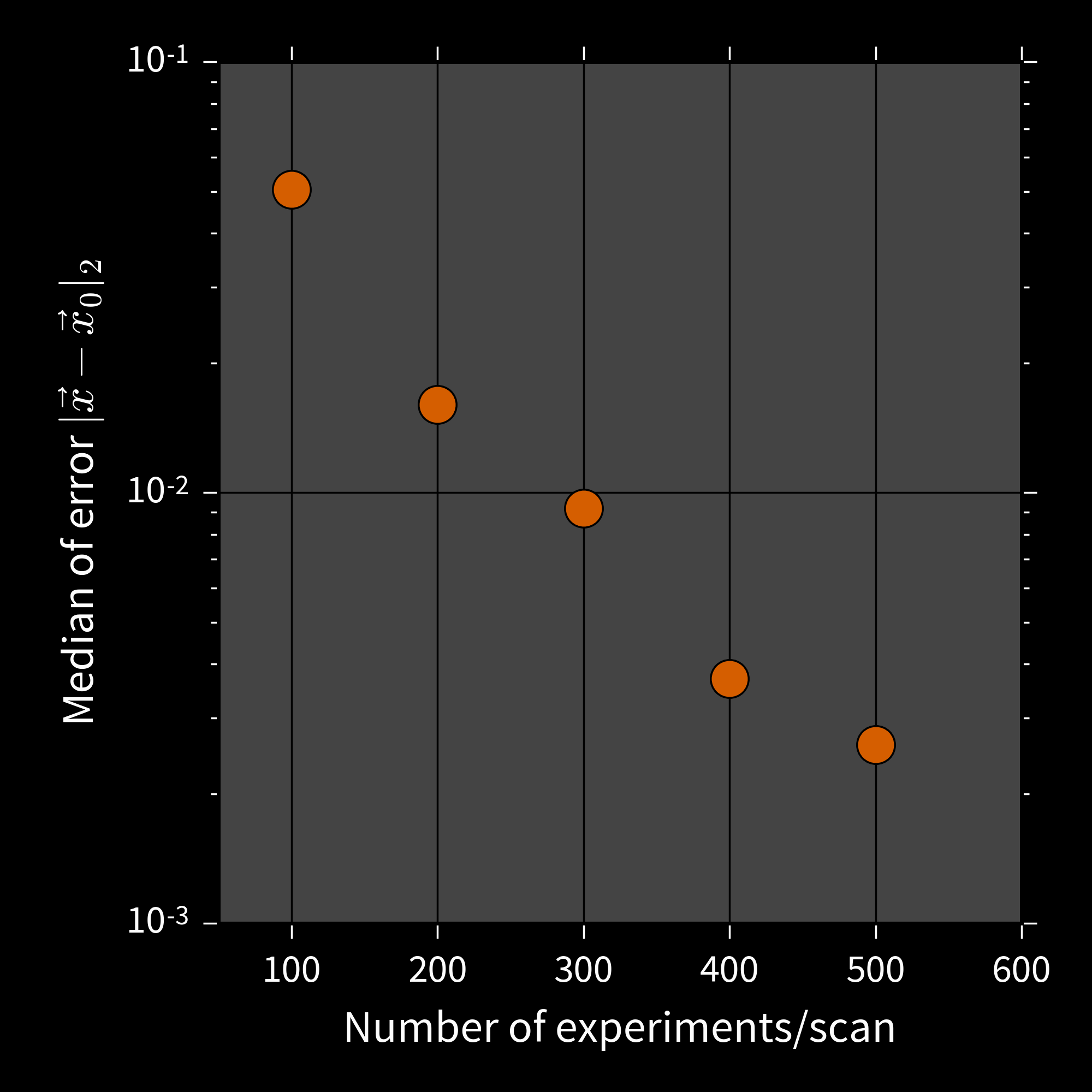
Filtering

Practical solution for current experimental tasks.
Enables learning large Hamiltonians using quantum resources.
Physical insight gives new statistical algorithm for even larger systems.

Going Further

Hyperparameterization Granade et al. s87: $\Pr(d | y) = \expect_x[\Pr(d | x) \Pr(x | y)]$.
Allows composing w/ noise, inhomogeneity, etc.
Model selection Ferrie 7nt: Using acceptance ratio or normalizations enables comparing models.
Quantum filtering Wiebe and Granade 1512.03145: Rejection filtering is a dequantization of quantum filtering using Harrow et al. bcz3hc.

Thank you!

Welford's Algorithm

Can compute $\bar{x}$, $\Sigma$ from one sample at a time. Numerically stable.

$n, \bar{x}, M_2 \gets 0$.
For each sample $x$:

$n \gets n + 1$ Record # of samples
$\Delta \gets x - \mu$ Diff to running mean
$\bar{x} \gets \bar{x} + \Delta / n$ Update running mean
$M_2 \gets M_2 + \Delta (x - \bar{x})$ Update running var

Return mean $\bar{x}$, variance $M_2 / (n - 1)$.

Vector case is similar.

We design experiments using the

PGH: Particle Guess Heuristic

Draw $\vec{x}_-, \vec{x}_-'$ from current posterior.
Let $t = 1 / |\vec{x}_- - \vec{x}_-'|$.
Return $e = (\vec{x}_-, t)$.

Adaptively chooses experiments such that
$t |\vec{x}_- - \vec{x}_-'| \approx\,$ constant.

Rejection and Particle Filtering for Hamiltonian Learning

What is a Hamiltonian?

Aside: Why Bayesian?

Example

Inference as an Iterative Algorithm

Rejection Sampling Isn't Enough

Example: Biased Coin $x = (p)$

Rejection Filtering (RejF)

Example: Phase Estimation, $x = (\phi)$

Applications

Example: Phase Estimation, $x = (\phi)$

Liu-West Resampler

Particle Filter

Useful for Hamiltonian models...

...as well as other QIP tasks.

Estimation in Practice

Error Bars

Time-Dependence

Bigger and Better

Simulation Costs

Example: Ising on Complete Graph

Quantum Bootstrapping

50 qubit Ising chain, 8 qubit simulator, 4 qubit observable

Filtering

Going Further

Thank you!

Welford's Algorithm

PGH: Particle Guess Heuristic