14 Sep 2019
Last week, I took a look at what a quantum state is in the context of quantum development, using Q# to get a handle on things.
Today, though, I’d like to take a little step back and look at what Q# is in the first place, as well as some things that Q# is not.
Q# is a Programming Langauge
When you get right down to it, quantum programs are classical programs that tell a quantum computer what to do.
After all, we want to be able to work with classical data, and to get classical data back out from our quantum computers.
From that perspective, then, it’s really important that Q# is a programming language.
For instance, a traditional “hello, world” application looks pretty much how you might expect a “hello, world” application to look:
namespace HelloWorld {
open Microsoft.Quantum.Intrinsic;
/// # Summary
/// Says hello to the world.
function Hello() : Unit {
Message("Hello, world!");
}
}
As a programming language, Q# builds on the long history of classical programming languages to make it as easy as possible to write quantum programs as well.
For example, throughout the history of classical programming, we’ve learned that features like namespaces and API documentation comments help us organizing and understanding our code; we can already see both features on display here in our “Hello, world” Q# program.
Q# is a Domain-Specific Language
Given that Q# is “just” a programming language, one might then ask why it exists at all.
We could in principle write our quantum programs in existing classical languages like Python, C#, Java, JavaScript, and so forth.
That said, each language we work with in software development is engineered to be good at different tasks, and to focus on different domains.
Q# is distinct from other programming languages in that it is designed from the first step to be great at writing quantum programs.
This means that Q# makes some choices as to what features to include and which features to leave out that are unusual for general-purpose classical languages, but that make it really easy to write rich quantum programs.
For example, since quantum mechanics is reversible, one common pattern in quantum programming is to run a subroutine backwards.
We may want to write a program that converts some quantum data into a representation where it’s easier to do a particular calculation, do that calculation, then undo our first transformation.
In Q#, this is supported by the Adjoint keyword, which represents the inverse of an operation.
Just as we can run PrepareEntangledState to entangle the state of some qubits, we can run Adjoint PrepareEntangledState to measure out that entanglement.
In order to support the Adjoint keyword, we need a few things to be true about our quantum programs:
- Loops can’t exit early, otherwise we couldn’t reverse the direction of a loop.
- Classical calculations used in a reversible operation need to be deterministic.
- Classical computations used in a reversible operation can’t have side effects.
To ensure these are all true, for loops work a bit differently in Q#, and there’s a difference between functions (which are always deterministic), and operations (which may have side effects, including sending instructions to a quantum device).
These choices made with the design of Q# help make it a perfect fit for what we need a quantum programming language to do.
If you’re interested in learning more about why we need Q#, check out Alan Geller’s post on the Q# dev blog.
Q# Includes Classical Logic
All the above being said, many quantum programs also include a lot of traditional, classical computation that has to work in close tandem with a quantum device.
From finding the right rotation angles to describe a quantum simulation task, through to using measurement data from a quantum device to decide the next measurement that you should do, quantum programming is rife with classical computational tasks.
This means that Q# has to not only be great at sending instructions to a quantum computer, but also at the kind of classical computations that need to run alongside a quantum device.
As a result, Q# includes a lot of features like user-defined types and functional programming libraries to help you write classical logic in your quantum programs.
Q# is Not a Circuit Language
It’s pretty common when talking about quantum programming to focus on a particular kind of quantum program called a circuit.
By analogy to a classical logic circuit, which describes how a bunch of different classical logic gates are connected to each other, a quantum circuit expresses a quantum program as a sequence of quantum gates.
This view has been really useful in quantum computing research for many years, but it has some problems that make it hard to use for developing quantum programs.
The most critical problem with thinking in terms of quantum circuits is that it’s really difficult to incorporate classical logic into a circuit diagram.
Classical logic circuits and quantum circuits are at best rough analogies to each other, and don’t really mix together.
By contrast, classical logic is really easy to write out.
For example, in quantum teleportation (a fancy and whimsical name for a neat way to move quantum data around), we need to apply quantum instructions based on the result of some measurements.
This is really easy to write in Q#:
if (MResetZ(msg) == One) { Z(target); }
if (MResetZ(register) == One) { X(target); }
This works because Q# isn’t a circuit description language, but something much more powerful: a language for expressing quantum algorithms in terms of quantum programs.
You Don’t Need to Know C# to Use Q#
Taking a turn for a moment, you might guess from the fact that “sharp” is right there in the name “Q#” that you need to know C# and .NET development to use Q#.
After all, over the 17 years that .NET has been around, “sharp” has become a pretty traditional indicator that something is a part of the .NET ecosystem: F#, SharpDevelop, Resharper, Gtk#, even A#, J#, P#, and X#!
In the case of Q#, though, what that “sharp” tells you is that Q# is built from and plays well with the .NET ecosystem.
Just as Q# has learned from the history of classical programming languages, Q# reuses a lot of .NET infrastructure like the NuGet package manager to make it easy easy as possible to write powerful quantum applications.
That doesn’t mean, however, you have to use C# or other .NET languages to write Q#.
Indeed, Q# provides interoperability with Python, making it easy to include Q# programs as a part of your data science or research workflow.
Q# can even be used entirely on its own from within Jupyter Notebook, thanks to the IQ# kernel for Jupyter.
Even if you want to use Q# with the cross-platform open-source .NET Core SDK, that doesn’t mean you need to be a C# expert.
It’s easy to use Q# from F#, Visual Basic .NET, and even PowerShell as well.
If you’re new to .NET entirely, the project templates, Visual Studio Code and Visual Studio 2019 extensions, and the Quantum Development Kit samples all make it really easy to use Q# with .NET.
When it comes down to it, Q# is meant to write quantum programs that work well with existing classical platforms.
Whether you’re a seasoned C# developer, or a die-hard Pythonista, whether you’re new to programming, or have been at this for a while, I encourage you to give Q# a try.
You Don’t Need to Know Quantum Computing to Get Started with Q#
OK, so you don’t have to be a .NET developer to start writing quantum programs, but surely you have to at least be pretty good at this quantum stuff, right?
Not really, as it turns out!
One of the most amazing things that has happened to quantum computing in the past few years is that it has gotten much easier to jump in, and to learn by doing.
Five or ten years ago, your best bet for getting involved with quantum computing probably would have started by reading a textbook and writing down a bunch of matrices, and probably even taking some graduate-level classes.
That’s still a great way to learn, but there’s a lot of other really good paths to learning quantum computing as well thanks to how much easier it has gotten to write and run quantum programs on your laptop or on the web.
Using tools like Q# and the Quantum Development Kit, you can try out your understanding by writing a quantum program, then you can run that program to see if it matched with your understanding.
The ability to quickly get feedback like this has really broadened the set of skills that can help you understand quantum computing.
The quantum computing community is bigger now than it ever has been, not just in terms of the number of people, but also in terms of the kinds of backgrounds that people bring with them to the community, the diversity of people in the community, and the ways of thinking about quantum computing.
Given that, if you’re looking to use Q# to learn quantum computing, where should you start?
I’m definitely partial to my own book, of course (new chapters coming soon!), but there’s a lot more out there as well.
Check out qsharp.community for a great list!
However you decide to learn about quantum computing, though, welcome to the community! 💕
I’m really excited for what you bring to quantum computing.
08 Sep 2019
The Map is Not The Territory
There’s a classic observation in philosophy that “the map is not the territory.”
Though it sounds obvious enough to take entirely for granted, this observation reminds us that there is a difference between the world around us and how we choose to represent that world on a map.
Depending on what we want to use the map for, we abstract away many different properties of the real world, such as reducing the amount of detail that we include (we clearly can’t include every object in the real world in our maps).
We may even add things to our map that don’t actually exist in the world, but that we find useful at a social level, such as national borders.
In all cases, we make these choices so that our model of the world (a map) lets us predict what will happen when walk around the world.
We can use those predictions to trade off different possible routes, guess at what might be an interesting place to visit, and so forth.

The lesson learned from separating maps from the world becomes far less obvious, however, when we are working with realities and abstractions that are less familiar to us.
It’s quite easy, for instance, for both newcomers and experienced quantum physicists to accidentally conflate a register of qubits with the model we use to predict what that register will do.
In particular, if we want to simulate how a quantum program transforms data stored in a register of qubits, we can write down a state vector for that register, then use a simulator to propagate that state vector through the unitary matrices for each instruction in our program.
As an example, we can use tools like Q# and the Quantum Development Kit to understand how a quantum program can cause two qubits in a quantum register to become entangled.
Using IQ# with Jupyter Notebook, we might something like the following (run online):
In [1]: open Microsoft.Quantum.Diagnostics;
... open Microsoft.Quantum.Measurement;
...
... operation DemonstrateEntanglement() : (Result, Result) {
... using ((left, right) = (Qubit(), Qubit())) {
... H(left);
... CNOT(left, right);
...
... DumpMachine();
...
... return (MResetZ(left), MResetZ(right));
... }
... }
Out[1]: DemonstrateEntanglement
Here, we’ve defined a new operation that asks for two qubits, then runs the H and CNOT instructions on those qubits.
The call to DumpMachine asks the simulator to tell us what information it uses internally to predict what those instructions do, so that when we do the measurements at the end of the program, the simulator knows what it should return.
Looking at the output of this dump, we see that the simulator represents left and right by the state $\left(\ket{00} + \ket{11}\right) / \sqrt{2}$:
In [2]: %simulate DemonstrateEntanglement
# wave function for qubits with ids (least to most significant): 0;1
∣0❭: 0.707107 + 0.000000 i == ***********
[ 0.500000 ] --- [ 0.00000 rad ]
∣1❭: 0.000000 + 0.000000 i ==
[ 0.000000 ]
∣2❭: 0.000000 + 0.000000 i ==
[ 0.000000 ]
∣3❭: 0.707107 + 0.000000 i == ***********
[ 0.500000 ] --- [ 0.00000 rad ]
Out[2]: (One, One)
It might be then tempting to conclude that left and right are the state $\left(\ket{00} + \ket{11}\right) / \sqrt{2}$, but this runs counter to what we learned from the example of separating maps of the world from the world itself.
To resolve this, it helps to think a bit more about what a quantum state is in the context of a quantum program.
For starters, if I give you a copy of the state of a quantum register at any point in a quantum program, you can predict what the rest of that quantum program will do.
Implicit in the word “copy,” however, is that the state of a quantum register is a classical description of that register.
After all, you can’t copy a register of qubits, so the fact that we can copy the state is a dead giveaway that state vectors are a kind of classical model.
That classical model is a pretty useful one, to be fair; it not only lets you simulate what a register of qubits will do, but also lets you prepare new qubits in the same way, using techniques like the Shende–Bullock–Markov algorithm (offered in Q# as the Microsoft.Quantum.Preparation.PrepareArbitraryState operation).
Put differently, while the No-Cloning Theorem tells us that we can’t copy the data encoded by a quantum register into a second register, we can definitely copy the set of steps we used to do that encoding, then use that recipe to prepare a second register.
Perhaps instead of saying the map is not the territory, then, we should say that the cake is not the recipe!
While I can use a recipe to prepare a new cake, and to understand what should happen if I follow a particular set of steps, it’s difficult to eat an abstract concept like a recipe and definitely not very tasty.
It’s also pretty difficult to turn one cake into two, but not that hard to bake a second cake following the same recipe.
The Cake is Not a Lie
Thinking of a quantum state as a kind of recipe I can use to prepare qubits, then, what good is a quantum program?
To answer that, let’s look at one more example in Q#:
In [3]: open Microsoft.Quantum.Diagnostics;
... open Microsoft.Quantum.Measurement;
... open Microsoft.Quantum.Arrays;
...
... operation DemonstrateMultiqubitEntanglement() : Result[] {
... using (register = Qubit[10]) {
... H(Head(register));
... ApplyToEach(CNOT(Head(register), _), Rest(register));
...
... DumpMachine();
...
... return ForEach(MResetZ, register);
... }
... }
If we were to run this one, the simulator would dump out a state with $2^{10} = 1,024$ amplitudes, but it’s much easier to read and understand what that program does by looking at the Q# source itself.
From that perspective, a quantum program can help us understand a computational task by compressing it down from a description purely in terms of state vectors, focusing back on what we actually want to achieve using a quantum device.
The simplest and by far the most effective way to both achieve this compression is to simply write down the instructions we need to send to a quantum device to prepare our qubits in a particular state.
Thus, instead of writing $\ket{+}$, for instance, we write down the program H(q).
Instead of writing down $\ket{++\cdots+}$, we write down ApplyToEach(H, qs).
Instead of writing down a state vector for each individual step in a phase estimation experiment, we write a program that calls EstimateEnergy.
This has the massive added advantage that we can optimize our quantum programs; that is, we can write down a sequence of instructions that utilizes what we know about the task we’re trying to achieve to use as few quantum instructions as possible.
Indeed, the cake–recipe distinction is especially important as we consider actual quantum devices.
In order to solve interesting computational problems using quantum computers, we want to be able to measure actual qubits, and get useful answers back.
At that scale, writing down and thinking only in terms of state vectors simply isn’t possible.
We need instead to focus on what we actually want to do with our qubits.
Once we do that, we’re in a much better spot to have our cake and eat it, too.
If you liked this post, you’ll love Learn Quantum Computing with Python and Q#, now in early access preview from Manning Publications.
Check it out!
03 Dec 2018
This post is a part of the Q# Advent Calendar, and is made available under the CC-BY 4.0 license. Full source code for this post is available on GitHub.
When we program a quantum computer, at the end of the day, we are interested in asking classical questions about classical data.
This is a large part of why we designed the Q# language to treat quantum computers as accelerators, similar to how one might use a graphics card or a field-programmable gate array (FPGA) to speed up the execution of classical algorithms.
One implication of this way of thinking about quantum programming, though, is that we need for our quantum programs to be able to integrate into classical data processing workflows.
Since the classical host programs for Q# are .NET programs, this means that we can use the power of the .NET Core platform to integrate with a wide range of different workflows.
For instance, the quantum chemistry library that is provided with the Quantum Development Kit includes a sample that uses PowerShell Core together with Q# to process cost estimates for chemistry simulations.
From there, cost estimation results can be exported to any of the formats supported by PowerShell Core, such as XML or JSON, or can be processed further using open-source PowerShell modules, such as ImportExcel.
In this post, I’ll detail how the PowerShell Core integration in the quantum chemistry sample works as an example of how to integrate Q# with other parts of the .NET ecosystem.
What is PowerShell Core?
First off, then, what is PowerShell anyway?
Like bash, tcsh, xonsh, fish, and many other shells, PowerShell provides a command-line interface for running programs on and managing your computer.
Like many shells, PowerShell allows you to pipe the output from one command to the next, making it easy to quickly build up complicated data-processing workflows in a compact manner.
Suppose, for instance, we want to find the number of lines of source code in all Q# files in a directory:
PS> cd Quantum/
PS> Get-ChildItem -Recurse *.qs | ForEach-Object { Get-Content $_ } | Measure-Object -Line
Lines Words Characters Property
----- ----- ---------- --------
7823
Where PowerShell differs from most shells, however, is that the data sent between commands by piping isn’t text, but .NET objects.
PS> $measurement = Get-ChildItem -Recurse *.qs | ForEach-Object { Get-Content $_ } | Measure-Object -Line;
PS> $measurement.GetType()
IsPublic IsSerial Name BaseType
-------- -------- ---- --------
True False TextMeasureInfo Microsoft.PowerShell.Commands.MeasureInfo
This means that we can not only call methods on PowerShell variables, but can access strongly-typed properties of variables.
PS> $measurement.Lines.GetType()
IsPublic IsSerial Name BaseType
-------- -------- ---- --------
True True Int32 System.ValueType
This in turn makes it easy to convert between different representations of our data, such as exporting to JSON or XML.
PS> $measurement | ConvertTo-Json
{
"Lines": 7823,
"Words": null,
"Characters": null,
"Property": null
}
PS> $measurement | ConvertTo-Xml -As String
<?xml version="1.0" encoding="utf-8"?>
<Objects>
<Object Type="Microsoft.PowerShell.Commands.TextMeasureInfo">
<Property Name="Lines" Type="System.Int32">7823</Property>
<Property Name="Words" Type="System.Nullable`1[[System.Int32, System.Private.CoreLib, Version=4.0.0.0, Culture=neutral, PublicKeyToken=7cec85d7bea7798e]]" />
<Property Name="Characters" Type="System.Nullable`1[[System.Int32, System.Private.CoreLib, Version=4.0.0.0, Culture=neutral, PublicKeyToken=7cec85d7bea7798e]]" />
<Property Name="Property" Type="System.String" />
</Object>
</Objects>
Historically, PowerShell was released as Windows PowerShell, and was based on the .NET Framework.
Two and a half years ago, PowerShell was ported to .NET Core and made available cross-platform as PowerShell Core.
PowerShell Core is now openly developed and maintained on GitHub at the PowerShell/PowerShell repository.
If you haven’t installed PowerShell Core already, the PowerShell team provides installers for Windows, many Linux distributions, and macOS.
If you are currently using PowerShell on Windows, but aren’t sure if you’re using Windows PowerShell or PowerShell Core, you can check your current edition by looking at the $PSVersionTable automatic variable:
PS> $PSVersionTable.PSEdition
This will output Desktop for Windows PowerShell, and will output Core for PowerShell Core.
Writing PowerShell Commands in C#
We can add new functionality to PowerShell by writing small commands, called cmdlets, as .NET classes.
Let’s see how this works by making a new C# class that rolls dice for us.
To get started, we need to make a new C# library using the .NET Core SDK:
PS> dotnet new classlib -lang C# -o posh-die
# The automatic variable $$ always resolves to the last argument of the previous command.
# In this case, we can use it to quickly jump to the "posh-die" directory.
PS> cd $$
This will make a new directory with a C# project file and a single C# source file, Class1.cs, that we can edit:
# gci is an alias for Get-ChildItem, which can be used in the same way as
# ls or dir, both of which are also aliases for Get-ChildItem.
PS> gci
Directory: C:\Users\cgranade\Source\Repos\QsharpBlog\2018\December\src\posh-die
Mode LastWriteTime Length Name
---- ------------- ------ ----
d----- 11/27/2018 1:25 PM obj
-a---- 11/27/2018 1:25 PM 85 Class1.cs
-a---- 11/27/2018 1:25 PM 145 posh-die.csproj
To make this a PowerShell-enabled library, we need to add the right NuGet package:
PS> dotnet add package PowerShellStandard.Library
This will make the System.Management.Automation namespace available, which has everything we need to write our own cmdlets.
Go on and add the following to Class1.cs:
using System;
using System.Linq;
// This namespace provides the API that we need to implement
// to interact with PowerShell.
using System.Management.Automation;
namespace Quantum.Advent.PoSh
{
// Each cmdlet is a class that inherits from Cmdlet, and is given
// a name with the CmdletAttribute attribute.
// Here, for instance, we define a new class that is exposed to
// PowerShell as the Get-DieRoll cmdlet.
[Cmdlet(VerbsCommon.Get, "DieRoll")]
public class GetDieRoll : Cmdlet
{
// Our cmdlet class can have whatever private member variables,
// just as any other C# class.
private Random rng = new Random();
// We can expose properties as command-line parameters using
// ParameterAttribute.
// For instance, this property is exposed as the -NSides command-
// line parameter, and allows the user to select what kind of die
// they want to roll.
[Parameter]
public int NSides { get; set; } = 6;
[Parameter]
public int NRolls { get; set; } = 1;
// The main logic to any cmdlet is implemented in the ProcessRecord
// method, which is called whenever the cmdlet receives new data from
// the pipeline.
protected override void ProcessRecord()
{
foreach (var idxRoll in Enumerable.Range(0, NRolls))
{
// The WriteObject method lets us send new data out to the
// pipeline. If there's no other commands to receive that data,
// then it is printed out to the console.
WriteObject(rng.Next(1, NSides + 1));
}
}
}
}
We can then build our new cmdlet like any other .NET Core project:
PS> dotnet build
Microsoft (R) Build Engine version 15.5.179.9764 for .NET Core
Copyright (C) Microsoft Corporation. All rights reserved.
Restore completed in 15.79 ms for C:\Users\cgranade\Source\Repos\QsharpBlog\2018\December\src\posh-die\posh-die.csproj.
posh-die -> C:\Users\cgranade\Source\Repos\QsharpBlog\2018\December\src\posh-die\bin\Debug\netstandard2.0\posh-die.dll
Build succeeded.
0 Warning(s)
0 Error(s)
When we call dotnet build, the .NET Core SDK places a new assembly in bin/Debug/netstandard2.0 that we can then import into PowerShell:
PS> Import-Module bin/Debug/netstandard2.0/posh-die.dll
PS> Get-DieRoll -NSides 4
2
Since this is a PowerShell cmdlet, we can pipe its output to any other PowerShell cmdlet.
For instance, we can check that the die is fair using Measure-Object:
PS> Get-DieRoll -NSides 6 -NRolls 1000 | Measure-Object -Average -Minimum -Maximum | ConvertTo-Json
{
"Count": 1000,
"Average": 3.402,
"Sum": null,
"Maximum": 6.0,
"Minimum": 1.0,
"Property": null
}
Calling into the Quantum Development Kit from PowerShell
Quantum coins are clearly better than classical dice, so let’s add a new cmdlet that exposes a quantum random number generator (QRNG) instead.
We can start by adding the Quantum Development Kit packages to our project:
PS> dotnet add package Microsoft.Quantum.Development.Kit --version 0.3.1811.1501-preview
PS> dotnet add package Microsoft.Quantum.Canon --version 0.3.1811.1501-preview
We can then add Q# sources to our project and use them from C#.
Let’s go on and add a simple QRNG to the project by making a new source file called Qrng.qs:
namespace Quantum.Advent.PoSh {
// The MResetX operation is provided by the canon, so we open that here.
open Microsoft.Quantum.Canon;
/// # Summary
/// Implements a quantum random number generator (QRNG) by preparing a qubit
/// in the |0⟩ state and then measuring it in the 𝑋 basis.
///
/// # Output
/// Either `0` or `1` with equal probability.
operation NextRandomBit() : Int {
mutable result = 1;
using (qubit = Qubit()) {
// We use the ternary operator (?|) to turn the Result from
// MResetX into an Int to match how the C# RNG works.
set result = MResetX(qubit) == One ? 1 | 0;
}
return result;
}
}
We can then call this operation from a new cmdlet.
Add the following new class to Class1.cs, along with a new using declaration for Microsoft.Quantum.Simulation.Simulators:
[Cmdlet(VerbsCommon.Get, "CoinFlip")]
public class GetCoinFlip : Cmdlet
{
[Parameter]
public int NFlips { get; set; } = 1;
protected override void ProcessRecord()
{
// This time we make a new target machine that we can use to run the
// QRNG.
using (var sim = new QuantumSimulator())
{
// The foreach loop is the same as before, except that we call into
// Q# in each iteration instead of calling methods of a Random
// instance.
foreach (var idxFlip in Enumerable.Range(0, NFlips))
{
WriteObject(NextRandomBit.Run(sim).Result);
}
}
}
}
Before proceeding, let’s make sure to unload the previous version of our posh-die assembly:
PS> Remove-Module posh-die
This will make sure that we can load the new version, and that your PowerShell session hasn’t locked the assembly file on disk.
That frees us up to rebuild the C# project for our PowerShell module, along with the new Q# code that we added above:
PS> dotnet build
Microsoft (R) Build Engine version 15.5.179.9764 for .NET Core
Copyright (C) Microsoft Corporation. All rights reserved.
Restore completed in 22.01 ms for C:\Users\cgranade\Source\Repos\QsharpBlog\2018\December\src\posh-die\posh-die.csproj.
posh-die -> C:\Users\cgranade\Source\Repos\QsharpBlog\2018\December\src\posh-die\bin\Debug\netstandard2.0\posh-die.dll
Build succeeded.
0 Warning(s)
0 Error(s)
Time Elapsed 00:00:01.20
When you try to import this module, however, you’ll get an error:
# ipmo is an alias for Import-Module.
PS> ipmo .\bin\Debug\netstandard2.0\posh-die.dll
ipmo : Could not load file or assembly 'Microsoft.Quantum.Simulation.Core, Version=0.3.1811.1501, Culture=neutral, PublicKeyToken=40866b40fd95c7f5'. The system cannot find the file specified.
At line:1 char:1
+ ipmo .\bin\Debug\netstandard2.0\posh-die.dll
+ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+ CategoryInfo : NotSpecified: (:) [Import-Module], FileNotFoundException
+ FullyQualifiedErrorId : System.IO.FileNotFoundException,Microsoft.PowerShell.Commands.ImportModuleCommand
What’s going on here?
The problem is that PowerShell couldn’t find the DLLs that make up the Quantum Development Kit.
Before, our project didn’t depend on anything else, but now we need to take one extra step of publishing after we build in order to put all the DLLs we need into the right place.
The .NET Core SDK makes this easy with the dotnet publish command.
Run the following, making sure to change win10-x64 to linux-x64 or osx-x64 as appropriate (for a full list of runtime IDs, see the .NET Core documentation):
PS> dotnet publish --self-contained -r win10-x64
We can then import the assembly as a PowerShell module the same way as before and run its cmdlets, just making sure to import the published assembly instead:
PS> ipmo .\bin\Debug\netstandard2.0\win10-x64\publish\posh-die.dll
PS> Get-CoinFlip -NFlips 10
Zero
One
One
Zero
Zero
One
Zero
Zero
Zero
One
PS> Get-CoinFlip -NFlips 1000 | Measure-Object -Maximum -Minimum -Average
Count : 1000
Average : 0.51
Sum :
Maximum : 1
Minimum : 0
Property :
There you go, that’s everything you need to get up and running using the Quantum Development Kit as a part of your PowerShell-based data processing workflows!
08 May 2017
Preamble
This post is a ♯longread primarily intended for graduate students and postdocs, but should hopefully be accessible more broadly.
Reading through the post should take about an hour, while following the instructions completely may take the better part of a day.
As an important caveat, much of what this post discusses is still experimental, such that you may run into minor issues in following the steps listed below.
I apologize if this happens, and thank you for your patience.
In any case, if you find this post useful, please cite it in papers that you write using these tools; doing so helps me out and makes it easier for me to write more such advice in the future.
Finally, we note that we have not covered several very important tools here, such as ReproZip.
This post is already over 6,000 words long, so we didn’t attempt to run through all possible tools.
We encourage further exploration, rather than thinking of this post as definitive.
Thanks for reading! ♥
Introduction
In my previous post, I detailed some of the ways our software tools and social structures encourage some actions and discourage others.
Especially when it comes to tasks such as writing reproducible papers that both offer to significantly improve research culture, but are somewhat challening in their own right, it’s critical to ensure that we positively encourage doing things a bit better than we’ve done them before.
That said, though my previous post spilled quite a few pixels on the what and the why of such encouragements, and of what support we need for reproducible research practices, I said very little about how one could practically do better.
This post tries to improve on that by offering a concrete and specific workflow that makes it somewhat easier to write the best papers we can.
Importantly, in doing so, I will focus on a paper-writing process that I’ve developed for my own use and that works well for me— everyone approaches things differently, so you may disagree (perhaps even vehemently) with some of the choices I describe here.
Even if so, however, I hope that in providing a specific set of software tools that work well together to support reproducible research, I can at least move the conversation forward and make my little corner of academia ever so slightly better.
Having said what my goals are with this post, it’s worth taking a moment to consider what technical goals we should strive for in developing and configuring software tools for use in our research.
First and foremost, I have focused on tools that are cross-platform: it is not my place nor my desire to mandate what operating system any particular researcher should use.
Moreover, we often have to collaborate with people that make dramatically different choices about their software environments.
Thus, we must be careful what barriers to entry we establish when we use methodologies that do not port well to platforms other than our own.
Next, I have focused on tools which minimize the amount of closed-source software that is required to get research done.
The conflict between closed-source software and reproducibility is obvious nearly to the point of being self-evident.
Thus, without being purists about the issue, it is still useful to reduce our reliance on closed-source gatekeepers as much as is reasonable given other constraints.
The last and perhaps least obvious goal that I will adopt in this post is that each tool we develop or adopt here should be useful for more than a single purpose.
Installing software introduces a new cognative load in understanding how it operates, and adds to the general maintenance cost we pay in doing research.
While this can be mitigated in part with appropriate use of package management, we should also be careful that we justify each piece of our software infrastructure in terms of what benefits it provides to us.
In this post, that means specifically that we will choose things that solve more than just the immediate problem at hand, but that support our research efforts more generally.
Without further ado, then, the rest of this post steps through one particular software stack for reproducible research in a piece by piece fashion.
I have tried to keep this discussion detailed, but not esoteric, in the hopes of making an accessible description.
In particular, I have not focused at all on how to develop scientific software of how to write reproducible code, but rather how to integrate such code into a high-quality manuscript.
My advice is thus necessarily specific to what I know, quantum information, but should be readily adapted to other fields.
Following that, I’ll detail the following components of a software stack for writing reproducible research papers:
- Command-line environment: PowerShell
- TeX / LaTeX distribution: TeX Live and MiKTeX
- Literate programming environment: Jupyter Notebook
- Text editor: Visual Studio Code
- LaTeX template:
{revtex4-1}, {quantumarticle}, and {revquantum}
- Project layout
- Version control: Git
- arXiv build management: PoShTeX
Command Line
Command-line interfaces and scripting languages provide a very powerful paradigm for automating disparate software tools into a single coherent process.
For our purposes, we will need to automate running TeX, running literate scientific computing notebooks, and packaging the results for publication.
Since these different software tools were not explicitly designed to work together, it will be easiest for our purposes to use a command-line scripting language to manage the entire process.
There are many compelling options out there, including celebrated and versatile systems such as bash, tcsh, and zsh, as well as newer tools such as fish and xonsh.
For this post, however, I will describe how to use Microsoft’s open-source PowerShell instead.
Microsoft offers PowerShell easy-to-install packages for Linux and macOS / OS X on at their GitHub repository.
For most Windows users, we don’t need to install PowerShell, but we will need to install a package manager to help us install a couple things later.
If you don’t already have Chocolatey, go on and install it now, following their instructions.
Similarly, we will use the package manager Homebrew for macOS / OS X.
The quickest way to install it is to run the following command in Terminal:
$ /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"
Also, be sure to restart your Terminal window after the installation.
Then, we install PowerShell with the following two commands:
$ brew tap caskroom/cask
$ brew cask install powershell
The first command installs the Homebrew Cask extension for programs distributed as binaries.
Aside: Why PowerShell?
As a brief aside, why PowerShell?
One of the long-standing annoyances to getting anything working in a reliable and cross-platform manner is that Windows is just not like Linux or macOS / OS X.
My interest here is not in saying that Windows is either good or bad, but to solve the problem of how to get things working across that divide in a reliable way.
Certainly, scripting languages like bash have been ported to Windows and work well there, but they don’t tend to work in a way that plays well with native tools.
For instance, it is difficult to get Cygwin Bash to reliably interoperate with commonly-used TeX distributions such as MiKTeX.
Many of these challenges arise from that bash and other such tools work by manipulating strings, rather than providing a typed programming environment.
Thus, any cross-platform portability must eventually deal with annoyances such as / versus \ in file name paths, while leaving slashes invariant in cases such as TeX source.
By contrast, PowerShell can be used as a command-line REPL (read-evaluate-print loop) interface to the more structrued .NET programming environment.
That way, OS-specific differences such as / versus \ can be handled as an API, rather than relying on string parsing for everything.
Moreover, PowerShell comes pre-installed on most recent versions of Windows, making it easier to deal with the comaprative lack of package management on most Windows installations.
(PowerShell even addresses this by providing some very nice package management features, which we will use in later sections.)
Since PowerShell has recently been open-sourced, we can readily rely on it for our purposes here.
TeX
For writing a reproducible scientific paper, there’s really no substitute still for TeX.
Thus, if you don’t have TeX installed already, let’s go on and install that now.
(Linux only) TeX Live
We can use Ubuntu’s package manager to easily install TeX Live:
$ sudo apt install texlive
The process will be slightly different on other variants of Linux.
(Windows only) MiKTeX
Since we installed Chocolatey earlier, it’s quite straightforward to install MiKTeX.
From an Administrator session of PowerShell (right-click on PowerShell in the Start menu, and press Run as administrator), run the following command:
(macOS / OS X only) MacTeX
Installing MacTeX is similarly straightforward using Homebrew Cask (which we should have installed earlier):
$ brew cask install mactex
Jupyter
Moving on, let’s take a few seconds to get Jupyter up and running.
Put succiently, Jupyter is a powerful infrastructure fo scientific programming in a variety of different languages.
Indeed, even the name points to the diversity of tools supported, as it originates from a portmanteau of Julia, Python and R.
Jupyter goes well beyond these three examples, though, and supports a language-agnostic interface for programming in JavaScript, F#, and even MATLAB.
Of particular interest to us is the Jupyter Notebook functionality, previously known as IPython Notebook.
This tool allows us to write literate documents that intersperse source code, explanations, mathematics, figures and plots.
As such, Jupyter Notebook is ideal for providing lucid and readable explanations of numerical and experimental results, providing a way to clearly explain a reproducible project.
Though Jupyter is a language-independent framework, the code infrastructure itself is written in Python.
Thus, the easiest way to get Jupyter in a cross-platform way is to install a distribution of Python, such as Anaconda, that incldues Jupyter as a package.
Since we want to focus in this post on how to write papers rather than on the programming aspects, we won’t go into detail at the moment on how to use Jupyter; below, we suggest some resources for getting started with Jupyter as a programming tool.
For now, we focus on getting Jupyter installed and running.
On Windows, we can again rely on Chocolatey:
PS> choco install anaconda3
On Linux and macOS / OS X, the process is not much more complicated.
To get started using Juyter Notebook, we suggest the following tutorial:
Editor
In keeping with our goals in the introduction, to actually write TeX source code, we don’t want a tool that works only for TeX.
Rather, we want something general-purpose that is also useful for TeX.
By doing so, we avoid the all-too-familiar workflow of using a specialized editor for each different part of a scientific project.
This way, increased familiarity and proficiency with our software tools benefits us across the board.
With that in mind, we’ll follow the example of Visual Studio Code, an open-source and cross-platform text editing and development platform from Microsoft.
Notably, many other good examples exist, such as Atom; we focus on VS Code here as an example rather than as a recommendation over other tools.
With that aside, let’s start by installing.
If you’re running on Ubuntu or macOS / OS X, let’s download Visual Studio Code from the VS Code website.
Alternatively for macOS / OS X, you can use Homebrew Cask
$ brew cask install visual-studio-code
On Ubuntu, we only need to install VS Code manually the first time; after that, Code can be managed using Ubuntu Software Center in the same manner as built-in packages.
Meanwhile, the macOS / OS X version is installed by dragging the downloaded app into Applications.
Once again, Chocolatey comes to the rescue for Windows users:
PS> choco install visualstudiocode
In any case, once we have VS Code installed, let’s install a few extensions that will make our lives much easier in the rest of this post.
Thankfully, this is quite straightforward due to the use of extension packs.
Roughly, an extension pack is a special kind of extension that does nothing on its own, but specifies a list of other extensions that should be installed.
I maintain a rudimentary example of such for use in scientific computing that includes some useful extensions for our purposes here.
To install it, press Ctrl+Shift+X (Windows and Linux) / ⌘+Shift+X (macOS / OS X) to open the Extensions panel, and search for cgranade.scicomp-extension-pack.
Though the full functionality exposed by these extensions is beyond the scope of this post, we’ll explore some important parts as we discuss other parts of our software stack.
For the most part, the extensions installed by the Scientific Computing Extension Pack do not need any configuration.
The exception is that for MiKTeX on Windows, the LaTeX Workshop extension needs to be configured to run texify instead of its default build engine of latexmk.
To do so press Ctrl+Shift+P / ⌘+Shift+P and type “Settings” until you are offered “Preferences: Open User Settings.”
Next, copy the following JavaScript Object Notation (JSON) code into your user settings:
"latex-workshop.latex.toolchain": [
{
"command": "texify",
"args": [
"--synctex",
"--tex-option=\"-interaction=nonstopmode\"",
"--tex-option=\"-file-line-error\"",
"--pdf",
"%DOC%.tex"
]
}
]
Getting forward and inverse search with SyncTeX working on Windows also takes a slight bit more work, as is documented on StackExchange.
This demonstrates one of the really neat features of modern editing platforms, by the way.
Namely, it’s very easy to share human-readable configuration snippets with others, making it easier to build a common platform with collegues and collaborators.
LaTeX Template
With the slight caveat that this section is the most specific to quantum information processing, we next turn our attention to the raison d’être for this whole endeavor: our LaTeX manuscript itself.
In doing so, we try to minimize the size of our initial template.
By minimizing the amount of boilerplate, we reduce the extent to which we introduce bugs in creating new manuscripts.
More importantly, though, keeping our template minimal reduces how much we have to understand in order to use and maintain it.
That said, we will generally have a lot of LaTeX code shared between projects.
To keep our manuscript templates minimal and free of boilerplate, then, we can rely on LaTeX’s document class and package functionality to abstract away this shared code.
For instance, the {revtex4-1} document class abstracts away much of the work involved in formatting a manuscript for physics papers, while the {quantumarticle} class does similar for the new Quantum journal.
Similarly, my own {revquantum} package attempts to abstract away much of the LaTeX code that I carry from project to project.
Though {revquantum} can be downloaded from the Comprehensive TeX Archive Network (CTAN), it will be easier for us to use Git to download the latest version.
We’ll install Git a bit later on in the post, so we’ll focus on the template for now and will install the required LaTeX packages once we have Git at our disposal.
Following that strategy, we can now write a very minimal LaTeX template:
\documentclass[aps,pra,twocolumn,notitlepage,superscriptaddress]{revtex4-1}
\usepackage[pretty,strict]{revquantum}
\newcommand{\figurefolder}{figures}
\begin{document}
\title{Example paper}
\date{\today}
\author{Cassandra Granade}
\affilEQuSUSyd
\affilUSydPhys
\begin{abstract}
\TODO
\end{abstract}
\maketitle
\bibliography{biblio}
\end{document}
Note that this template strips down the preamble (that is, the part of the LaTeX document before \begin{document}) to just three lines:
\documentclass[aps,pra,twocolumn,notitlepage,superscriptaddress]{revtex4-1}:
Declares the document class to be {revtex4-1} and specifies some reasonable default options.
Note that if an option isn’t specified for the society, journal or font size, {revtex4-1} will raise warnings.
Thus, by specifying a few options, we reduce the number of spurious warnings that we have to sort through.\usepackage[pretty,strict]{revquantum}:
Includes the {revquantum} package with modern typesetting options.
The strict option instructs {revquantum} to promote package incompatability warnings to errors, such that the manuscript will refuse to compile if there are issues with {revtex4-1} compatability.\newcommand{\figurefolder}{.}:
We’ll see more about this in the rest of the post, but roughly this command lets us abstract away details of our project structure from our LaTeX source.
That in turn will make it much easier to rearrange the project folder as need be, as only minimal changes will be required in the LaTeX source itself.
Project Layout
Now that we have a reasonable template in place for our paper, let’s proceed to make and layout a folder for our project.
The project folder needs to have somewhere to store the TeX source we use in typesetting the paper, and will likely need somewhere to store figures as well.
Assuming we have either numerics or an experiment in our paper, we will also need somewhere to put our Jupyter Notebooks and any other source files that they rely upon.
Putting these needs together, my projects often wind up looking something like this:
project/
tex/
project.tex:
Main TeX source file.project.bib:
Bibliography for main TeX source.revquantum.sty:
A copy of the {revquantum} package.
We will download and build {revquantum} later in this post.
fig/
*.pdf:
PDF-formatted figures for use in the main body.
src/
project.ipynb:
Main literate notebook for the project.*.py:
One or two miscellaneous Python modules needed for the main notebook.
data/:
Folder for experimental data generated by src/project.ipynb.
NB: do not use NumPy’s *.npz format for uploading data to arXiv as ancillary material, as this is not supported by arXiv.
Consider using HDF5 or similar instead.
If your data set is moderately-sized (> 6 MiB), then consider uploading to an external service such as Figshare instead of arXiv— this also makes it easier to use other data storage formats..gitignore:
A list of files, folders, and patterns to be excluded from version control.
Don’t worry about this for now, we’ll deal with it below.README.md:
Brief instructions on how to use the ancillary files provided with the paper.environment.yml or requirements.txt:
Software dependencies needed by the project.
How these files work is fairly specific to programming in Python, so we won’t go into the details here, but they make it easy for both collaborators and readers to quickly set up the software environment they need to run your code.
For more details, please see the documentation for pip and conda env.Export-ArXiv.ps1:
Build manifest for exporting the paper to an arXiv-formatted ZIP archive.
Later in the post, we’ll detail what this file should contain and how to use it.
For now, just make a blank text file with this name.
As with everything else in this post, you may want to layout your project differently than I’ve suggested here.
For instance, we included a copy of revquantum.sty above, since that’s not part of the “standard” set of packages installed on arXiv; if you depend on any other custom packages or classes, those would also appear in your layout.
If you have more than one or two other source files in src/, you may also want to make a package and distribute it separately from your paper.
You may also have additional files that you need to include, such as instrument configuration files.
It’s also common to have other folders like notes/ to keep rough or unfinished derivations, or refereeing/ to draft correspondance with referees and editors once you submit your paper.
What’s essential, though, is that no matter how you layout your project, you use the layout as consistantly as possible.
Doing so ensures that a file you need can always be found in the least surprising place, minimizing the amount of thought you have to spare on searching your folder structure.
Importantly, if this means you need to change your layout as your project itself changes, that is a fine and useful thing to do.
Your layout should, above all else, work for you and your collaborators with as little friction and additional thought as is reasonable.
Version Control
Once you’ve made a project folder, we need to be able to track how it changes over time and to share it with collaborators.
Though file-synchronization tools such as Dropbox, Google Drive, and OneDrive are commonly used for this task, they introduce a lot of additional maintenance costs that we would like to avoid.
For instance, it’s very difficult to collaborate using such services— conflicting edits are normally applied with preference only to whichever edits happened last, making it easy to accidently lose important edits.
Similarly, it’s hard to look at a source file and understand why a particular set of changes was made, such that it’s again too easy to accidentally undo edits from collaborators.
In keeping with the goals laid out at the start of the post, then, we’ll adopt distributed version control as a tool to enable collaboration and version tracking.
In particular, we will use Git in no small part due to its popularity, such that we can build off a large set of community-developed tools and services.
Git is a very useful tool in general, such that we again avoid overly-specialized software infrastructure.
I won’t lie: there is a learning curve to Git, such that initially it will take substantially longer to do research backed by Git than by file-synchronization tools.
In fairly short order, however, learning Git pays for itself both by avoiding common pitfalls introduced by file-synchronization tools and by providing powerful automation for other tasks outside the synchronization model.
Both the learning curve and the power of Git stem from the same source, in that Git is extremely reticent to erase any set of changes, no matter how insignificant.
For instance, if two contradictory sets of changes are made to a file, Git will demand that you explicitly specify how to merge them, rather than automatically overwritting changes that may be significant.
We won’t cover how to use Git in this post, but rather will focus on how to install it and configure it for setting up a reproducible paper.
In lieu, we recommend the following tutorials:
In following these tutorials, we recommend starting by using the command line as much as possible, as this helps build the volcabulary needed when working with graphical interfaces to Git.
In any case, let’s go on and install Git.
We will install Secure Shell (SSH) while we’re at it, since this is a very common and powerful way of interfacing with Git hosting providers such as GitHub, Bitbucket, and GitLab.
Notably, SSH is also very useful for other research tasks such as managing cluster resources and running Jupyter Notebooks on remote servers, such that in installing SSH we get access to another general-purpose tool.
On Windows, run the following in an Administrator PowerShell session:
PS> choco install git putty poshgit
If you haven’t already done so, you’ll need to set PuTTY to be the SSH implementation used by Git for Windows.
From within PowerShell, run the following:
PS> [Environment]::SetEnvironmentVariable("GIT_SSH", (Get-Command plink.exe | Select-Object -ExpandProperty Definition), "User")
If this doesn’t work, it’s likely because Get-Command plink.exe was unable to find the plink.exe command that comes with PuTTY.
This can happen, for instance, if the $Env:PATH environment variable was changed by choco install but not in your current PowerShell session.
The easiest way to fix this is to close and re-open your PowerShell session.
Notice that we’ve also installed poshgit (short for PowerShell Git) with this command, as that handles a lot of nice Git-related tasks within PowerShell.
To add posh-git to your prompt, please see the instructions provided with posh-git.
One of the more useful effects of adding posh-git to your prompt is that posh-git will then look at your setting for $Env:GIT_SSH and automatically manage your PuTTY configuration for you.
On Ubuntu, run the following in your favorite shell:
$ sudo apt install ssh git
This may warn that some or all of the needed packages are already installed— if so, that’s fine.
On macOS / OS X, SSH is pre-installed by default. To install Git, run git at the terminal and follow the installation prompts.
However, the versions of ssh and git distributed with macOS / OS X are often outdated.
Homebrew to the rescue:
Note that posh-git also partially works on PowerShell for Linux and macOS / OS X, but does not yet properly handle setting command-line prompts.
Once everything is installed, simply run git init from within your project folder to turn your project into a Git repository.
Use git add and git commit, either at the command line or using your editor’s Git support, to add your initial project folder to your local repository.
The next steps from here depend somewhat on which Git hosting provider you wish to use, but proceed roughly in four steps:
- Create a new repository on your hosting provider.
- Configure your SSH private and public keys for use with your hosting provider.
- Add your hosting provider as a
git remote to your local project.
- Use
git push to upload your local repository to the new remote.
Since the details depend on your choice of provider, we won’t detail them here, though some of the tutorials provided above may be useful.
Rather, we suggest following documentation for the hosting provider of your choice in order to get up and running.
In any case, as promised above, we can now use Git to download and install the LaTeX packages that we require.
To get {revquantum}, we’ll run the included PowerShell installer.
Note that, due to a bug that installer (currently being fixed), this will fail unless you already have Pandoc installed.
Thus, we’ll go on and work around that bug for now by installing Pandoc (besides, it’s useful in writing responses to referees, as I’ll discuss in a future post):
# macOS
$ brew install pandoc
# Ubuntu
$ sudo apt install pandoc
# Windows
PS> choco install pandoc
I sincerely apologize for this bug, and will have it fixed soon.
In any case, and having apologized for introducing additional requirements, let’s go on and install the packages themselves:
PS> git clone https://github.com/cgranade/revquantum.git
PS> cd revquantum
PS> # Only run the following on Windows, as Unblock-File isn't needed
PS> # on Linux and macOS / OS X.
PS> Unblock-File Install.ps1 # Marks that the installer is safe to run.
PS> ./Install.ps1
Installing the {quantumarticle} document class proceeds similarly:
PS> git clone https://github.com/cgogolin/quantum-journal.git
PS> cd quantum-journal
PS> # Only run the following on Windows, as Unblock-File isn't needed
PS> # on Linux and macOS / OS X.
PS> Unblock-File install.ps1 # NB: "install" is spelled with a lower-case i here!
PS> ./install.ps1
Note that in the above, we used HTTPS URLs instead of the typical SSH.
This allows us to download from GitHub without having to set up our public keys first.
Since at the moment, we’re only interested in downloading copies of {revquantum} and {quantumarticle}, rather than actively developing them, HTTPS URLs work fine.
That said, for your own projects or for contributing changes to other projects, we recommend taking the time to set up SSH keys and using that instead.
Aside: Working with Git in VS Code
As another brief aside, it’s worth taking a moment to see how Git can help enable collaborative and reproducible work.
The Scientific Computation Extension Pack for VS Code that we installed earlier includes the amazingly useful Git Extension Pack maintained by Don Jayamanne, which in turn augments the already powerful Git tools built into Code.
For instance, the Git History extension provides us with a nice visualization of the history of a Git repository.
Press Ctrl/⌘+Shift+P, then type “log” until you are offered “Git: View History (git log).”
Using this on the QInfer repository as an example, I am presented with a visual history of my local repository:
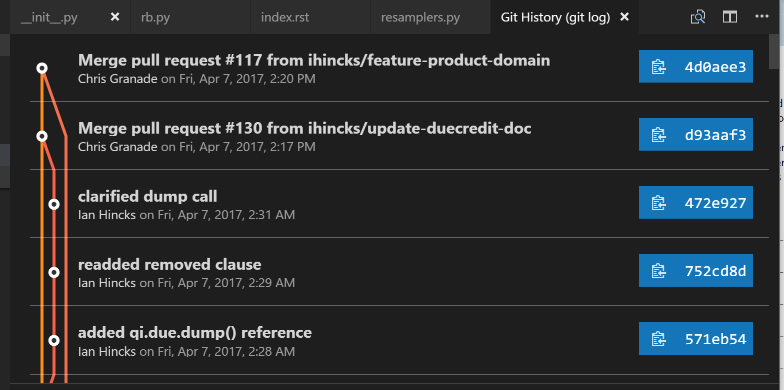
Clicking on any entry in the history visualization presents me with a summary of the changes introduced by that commit, and allows us to quickly make comparisons.
This is invaluable in answering that age old question, “what the heck did my collaborators change in the draft this time?”
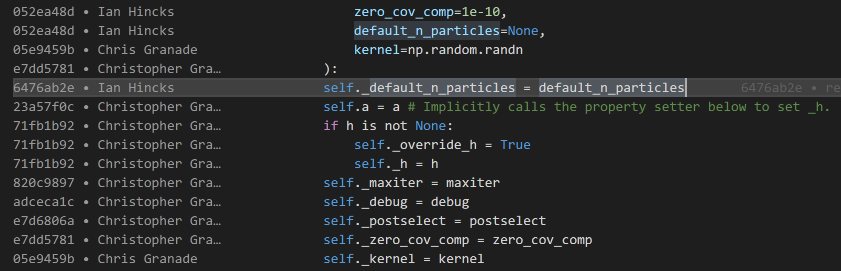
Somewhat related is the GitLens extension, which provides inline annotations about the history of a file while you edit it.
By default, these annotations are only visible at the top of a section or other major division in a source file, keeping them unobtrusive during normal editing.
If you temporarily want more information, however, press Alt+B to view “blame” information about a file.
This will annotate each line with a short description of who edited it last, when they did so, and why.
The last VS Code extension we’ll consider for now is the Project Manager extension, which makes it easy to quickly switch between Git repositories and manage multiple research projects.
To use it, we need to do a little bit of configuration first, and tell the extension where to find our projects.
Add the following to your user settings, changing paths as appropriate to point to where you keep your research repositories:
"projectManager.git.baseFolders": [
"C:\\users\\cgranade\\academics\\research",
"C:\\users\\cgranade\\software-projects"
]
Note that on Windows, you need to use \\ instead of \, since \ is an escape character.
That is, \\ indicates that the next character is special, such that you need two backslashes to type the Windows path separator.
Once configured, press Alt+Shift+P to bring up a list of projects.
If you don’t see anything at first, that’s normal; it can take a few moments for Project Manager to discover all of your repositories.
Aside: Viewing TeX Differences as PDFs (Linux and macOS / OS X only)
One very nice advantage of using Git to manage TeX projects is that we can use Git together with the excellent latexdiff tool to make PDFs annotated with changes between different versions of a project.
Sadly, though latexdiff does run on Windows, it’s quite finnicky to use with MiKTeX.
(Personally, I tend to find it easier to use the Linux instructions on Windows Subsystem for Linux, then run latexdiff from within Bash on Ubuntu on Windows.)
In any case, we will need two different programs to get up and running with PDF-rendered diffs.
Sadly, both of these are somewhat more specialized than the other tools we’ve looked at, violating the goal that everything we install should also be of generic use.
For that reason, and because of the Windows compatability issues noted above, we won’t depend on PDF-rendered diffs anywhere else in this post, and mention it here as a very nice aside.
That said, we will need by latexdiff itself, which compares changes between two different TeX source versions, and rcs-latexdiff, which interfaces between latexdiff and Git.
To install latexdiff on Ubuntu, we can again rely on apt:
$ sudo apt install latexdiff
For macOS / OS X, the easiest way to install latexdiff is to use the package manager of MacTeX.
Either use Tex Live Utiliy, a GUI program distributed with MacTeX or run the following command in a shell
$ sudo tlmgr update --self
$ sudo tlmgr install latexdiff
For rcs-latexdiff, I recommend the fork maintained by Ian Hincks.
We can use the Python-specific package manager pip to automatically download Ian’s Git repository for rcs-latexdiff and run its installer:
$ pip install git+https://github.com/ihincks/rcs-latexdiff.git
Once you have latexdif and rcs-latexdiff installed, we can make very professional PDF renderings by calling rcs-latexdiff on different Git commits.
For instance, if you have a Git tag for version 1 of an arXiv submission, and want to prepare a PDF of differences to send to editors when resubmitting, the following command often works:
$ rcs-latexdiff project_name.tex arXiv_v1 HEAD
Sometimes, you may have to specify options such as --exclude-section-titles due to compatability with the \section command in {revtex4-1} and {quantumarticle}.
arXiv Build Management
Ideally, you’ll upload your reproducible research paper to the arXiv once your project is at a point where you want to share it with the world.
Doing so manually is, in a word, painful.
In part, this pain originates from that arXiv uses a single automated process to prepare every manuscript submitted, such that arXiv must do something sensible for everyone.
This translates in practice to that we need to ensure that our project folder matches the expectations encoded in their TeX processor, AutoTeX.
These expectations work well for preparing manuscripts on arXiv, but are not quite what we want when we are writing a paper, so we have to contend with these conventions in uploading.
For instance, arXiv expects a single TeX file at the root directory of the uploaded project, and expects that any ancillary material (source code, small data sets, videos, etc.) are in a subfolder called anc/.
Perhaps most difficult to contend with, though, is that arXiv currently only supports subfolders in a project if that project is uploaded as a ZIP file.
This implies that if we want to upload even once ancillary file, which we certiantly will want to do for a reproducible paper, then we must upload our project as a ZIP file.
Preparing this ZIP file is in principle easy, but if we do so manually, it’s all too easy to make mistakes.
To rectify this and to allow us to use our own project folder layouts, I’ve written a set of commands for PowerShell collectively called PoShTeX to manage building arXiv ZIP archives.
From our perspective in writing a reproducible paper, we can rely on PowerShell’s built-in package management tools to automatically find and install PoShTeX if needed, such that our entire arXiv build process reduces to writing a single short manifest file then running it as a PowerShell command.
Let’s look at an example manifest.
This particular example comes from an ongoing research project with Sarah Kaiser and Chris Ferrie.
#region Bootstrap PoShTeX
$modules = Get-Module -ListAvailable -Name posh-tex;
if (!$modules) {Install-Module posh-tex -Scope CurrentUser}
if (!($modules | ? {$_.Version -ge "0.1.5"})) {Update-Module posh-tex}
Import-Module posh-tex -Version "0.1.5"
#endregion
Export-ArXivArchive @{
ProjectName = "sgqt_mixed";
TeXMain = "notes/sgqt_mixed.tex";
RenewCommands = @{
"figurefolder" = ".";
};
AdditionalFiles = @{
# TeX Stuff #
"notes/revquantum.sty" = "/";
"figures/*.pdf" = "figures/";
# "notes/quantumarticle.cls" = $null
# Theory and Experiment Support #
"README.md" = "anc/";
"src/*.py" = "anc/";
"src/*.yml" = "anc/";
# Experimental Data #
"data/*.hdf5" = "anc/";
# Other Sources #
# We include this build script itself to provide an example
# of using PoShTeX in pactice.
"Export-ArXiv.ps1" = $null;
};
Notebooks = @(
"src/experiment.ipynb",
"src/theory.ipynb"
)
}
Breaking it down a bit, the section of the manifest between #region and #endregion is responsible for ensuring PoShTeX is available, and installing it if not.
This is the only “boilerplate” to the manifest, and should be copied literally into new manifest files, with a possible change to the version number "0.1.5" that is marked as required in our example.
The rest is a call to the PoShTeX command Export-ArXivArchive, which produces the actual ZIP given a description of the project.
That description takes the form of a PowerShell hashtable, indicated by @{}.
This is very similar to JavaScript or JSON objects, to Python dicts, etc.
Key/value pairs in a PowerShell hashtable are separated by ;, such that each line of the argument to Export-ArXivArchive specifies a key in the manifest.
These keys are documented more throughly on the PoShTeX documentation site, but let’s run through them a bit now.
First is ProjectName, which is used to determine the name of the final ZIP file.
Next is TeXMain, which specifies the path to the root of the TeX source that should be compiled to make the final arXiv-ready manuscript.
After that is the optional key RenewCommands, which allows us to specify another hashtable whose keys are LaTeX commands that should be changed when uploading to arXiv.
In our case, we use this functionality to change the definition of \figurefolder such that we can reference figures from a TeX file that is in the root of the arXiv-ready archive rather than in tex/, as is in our project layout.
This provides us a great deal of freedom in laying out our project folder, as we need not follow the same conventions in as required by arXiv’s AutoTeX processing.
The next key is AdditionalFiles, which specifies other files that should be included in the arXiv submission.
This is useful for everything from figures and LaTeX class files through to providing ancillary material.
Each key in AdditionalFiles specifies the name of a particular file, or a filename pattern which matches multiple files.
The values associated with each such key specify where those files should be located in the final arXiv-ready archive.
For instance, we’ve used AdditionalFiles to copy anything matching figures/*.pdf into the final archive.
Since arXiv requires that all ancillary files be listed under the anc/ directory, we move things like README.md, the instrument and environment descriptions src/*.yml, and the experimental data in to anc/.
Finally, the Notebooks option specifies any Jupyter Notebooks which should be included with the submission.
Though these notebooks could also be included with the AdditionalFiles key, PoShTeX separates them out to allow passing the optional -RunNotebooks switch.
If this switch is present before the manifest hashtable, then PoShTeX will rerun all notebooks before producing the ZIP file in order to regenerate figures, etc. for consistency.
Once the manifest file is written, it can be called by running it as a PowerShell command:
This will call LaTeX and friends, then produce the desired archive.
Since we specified that the project was named sgqt_mixed with the ProjectName key, PoShTeX will save the archive to sgqt_mixed.zip.
In doing so, PoShTeX will attach your bibliography as a *.bbl file rather than as a BibTeX database (*.bib), since arXiv does not support the *.bib → *.bbl conversion process.
PoShTeX will then check that your manuscript compiles without the biblography database by copying to a temporary folder and running LaTeX there without the aid of BibTeX.
Thus, it’s a good idea to check that the archive contains the files you expect it to by taking a quick look:
Here, ii is an alias for Invoke-Item, which launches its argument in the default program for that file type.
In this way, ii is similar to Ubuntu’s xdg-open or macOS / OS X’s open command.
Once you’ve checked through that this is the archive you meant to produce, you can go on and upload it to arXiv to make your amazing and wonderful reproducible project available to the world.
Conclusions and Future Directions
In this post, we detailed a set of software tools for writing and publishing reproducible research papers.
Though these tools make it much easier to write papers in a reproducible way, there’s always more that can be done.
In that spirit, then, I’ll conclude by pointing to a few things that this stack doesn’t do yet, in the hopes of inspiring further efforts to improve the available tools for reproducible research.
- Template generation:
It’s a bit of a manual pain to set up a new project folder.
Tools like Yeoman or Cookiecutter help with this by allowing the development of interactive code generators.
A “reproducible arXiv paper” generator could go a long way towards improving practicality.
- Automatic Inclusion of CTAN Dependencies:
Currently, setting up a project directory includes the step of copying TeX dependencies into the project folder.
Ideally, this could be done automatically by PoShTeX based on a specification of which dependencies need to be downloaded, a la pip’s use of
requirements.txt.
- arXiv Compatability Checking:
Since arXiv stores each submission internally as a
.tar.gz archive, which is inefficient for archives that themselves contain archives, arXiv recursively unpacks submissions.
This in turn means that files based on the ZIP format, such as NumPy’s *.npz data storage format, are not supported by arXiv and should not be uploaded.
Adding functionality to PoShTeX to check for this condition could be useful in preventing common problems.
In the meantime, even in lieu of these features, I hope that this description is a useful resource. ♥
Acknowledgements
31 Mar 2017
- What we encourage and incentivize has consequences, both direct and unseen.
- Those incentives often preclude progress on things we claim to value in academic research.
- Better tools and better institutional support can help.
- Hey, I made some crappy tools to point to a couple examples of incentives against reproducible research.
Incentives
To a large extent, we do what we are encouraged to do. We are after all, more or less social agents, and respond the people and social systems around us as social agents. Examining what we are encouraged to do, and how we build incentive structures to reward some actions and people over others, is thus a matter of perpetual importance. To take one particularly stark example, I have argued here before that sexual harassment and discrimination are at least as pervasive in physics as in many other fields of research. One way to combat this, then, is to develop incentive structures that do not further reinforce inequality but instead make it more difficult to use scientific institutions to harass and attack. Thus, we can use tools such as codes of conduct, effective reporting at institutions, and backchannel communication to build better systems of incentives that encourage positive behavior. As a side note, this is especially critical as science funding is under imminent and unprecedented attack in the United States— we’ve seen that public outcry can have magnificent effects for protecting institutions and funding, such that we must ensure that we earn the public support we now so existentially require.
Having thus seen that systems of encouragement can be social, it’s also important to realize that encouragement can come as well in the form of technical constraints imposed by the systems that we build and interact with. To take one particular and relatively small example, the one-function-per-file design decision of MATLAB encourages users to write longer functions than they might otherwise in a different language. In turn, this makes it harder for MATLAB users to transfer skills to software development in other languages, discouraging diversity in software tools.
Even though the design decisions made by MATLAB can be often be circumvented by users who disagree, they has a significant impact on what kind of software design decisions get made. For instance, using MATLAB affects how code is shared as well as how APIs are designed. These decisions can in turn also compound with social encouragements; consider the magnification of this example, given the near-exclusive focus on proprietary tools such as MATLAB found in many undergraduate physics programs. That is, our approach to physics education encourages certain software development methodologies over others as an immediate consequence of teaching particular tools rather than methods.
The interaction between social and technical encouragements is widely recognized. In user interface and user experience design, for instance, the concept of an affordance is used to encourage a user to some set of interactions with a technical system. This understanding can be leveraged as a powerful tool for persuading users both to benefitial and malicious ends, as has been prominently argued for at least fifteen years. Critically reflecting on how social and technical encouragements combine to affect our behavior is accordingly a pressing issue across different disciplines.
State of the Art
Examining physics methodologies in detail from the perpsective of incentives, let’s then consider what kinds of encouragement we create with our design choices and with our research methodologies by examining a few relevant examples. Importantly, none of these examples represent criticism of individual users or research groups, but rather an examination of what incentives users and groups are under.
-
Experiment control and analysis: Current expeirmental methodology in physics often concerns itself with ad hoc control systems developed internally by graduate and undergraduate students in a single group. This discourages collaboration between groups using different internal systems, and more critically, can discourage challenging assumptions built in to early stages of experimental control systems. Efforts such as InstrumentKit, Qudi, and QCoDeS, Instrumental, SpanishAquisition, and Labscript have attempted to change these incentives by instead providing high-quality open source libraries that can work across groups, and hence remove disincentives that can impede collaboration. Collecting common functionality in this way also encourages contributing safety and correctness features that would otherwise be undervalued in a single ad hoc application.
-
Statistical analysis: Common software tools such as MATLAB, SciPy, and Mathematica all provide “curve fitting” functionality by default, and report frequentist metrics on the results produced by “curve fitting.” This ready availability encourages the use of “fitting” over other methodologies, even in cases where the theory behind “fitting” does not apply. Taken in conjunction with the reticence of reviewers to point out such methological problems, it isn’t a stretch to say that we directly encourage the publication of incorrect research results by failing to provide easy-to-use and principled statistical analysis tools that match experimental models.
-
Collaboration and version control: At least ideally, collaboration forms a cornerstone of scientific research. Accordingly, the writing and editing of research manuscripts is also ideally a collaborative effort. To support that, we often employ software tools such as Dropbox to synchronize changes between collaborators. The technical restrictions imposed by Dropbox, however, present their own encouragements and discouragements. For example, that Dropbox will overwrite changes made concurrently by two users discourages authors from editing on disjoint sections. Often, this is mitigated by social agreements such as “tokens,” where authors agree only to edit a work if they hold the “token” for the TeX source. That Dropbox does not present version history in a consise and readable form also discourages focusing editing efforts on recent changes. The eagerness of Dropbox to share temporary and editor-specific files also discourages the use of modern text editors such as Atom, Sublime Text and VS Code, each of which uses machine-specific metadata to store information such as undo history. Though these issues can somewhat be mitigated by using formal version control systems such as Git or Mercurial, that many students and postdocs have little to no opportunity to learn such tools presents a strong social discouragement against robust and efficient collaboration.
-
Plotting and accessibility: Approximately 10% of the population is at least mildly color-blind such that the use of colors in scientific visualizations can prevent a significant barrier to accessibility. Default color schemes in widely-used tools such as MATLAB discourage accessible design by forcing users to specify that each plot individually should use an accessible palette. Up until recently, the Matplotlib plotting library for Python has similarly discouraged accessible design, though other positive encouragements such as declarative style sheets have somewhat mitigated this.
Open Science
One critical component common to each of these examples is that they use the concept of open source software development to change the incentives for researchers. If it becomes easier — if we encourage — contributing to existing efforts instead of reinventing well-understood wheels, then not only does it become less expensive to do cutting-edge research, but it also becomes more practical to do reproducible research. As we can see from reproducibility crises in other fields, physics research likely cannot survive its current model of closed-source closed-data closed-analysis papers hidden behind increasingly-expensive paywalls. Perhaps most critically, the lack of reproducibility in scientific papers can also play a role in exacerbating public mistrust of science. I’ll return to the role that the arXiv plays in changing these incentives later, but suffice to say that open access is not sufficient to imply that a paper or other research output can be independently assessed for correctness. The gap between the openness we currently take as being standard in physics and the level of transparency that we need is thus not a trivial one.
In this discussion, of course, we also cannot afford to elide that open science in general and open source in particular also helps to remove elements of gatekeeping that can be used to preclude participation. In current practice, the expense of performing physics research, be it theory or experiment, naturally concentrates decision-making power in a smaller number of individuals. Though the effects of this concentration can be mitigated to some degree, it is also important to reduce the areas in which cognative biases can hide from critical examination. Reducing barriers to entry can provide a way to do so.
I posit that these self-same barriers to entry are, perhaps ironically, one of the largest impediments to the adoption of open science methodologies in physics. Take, for instance, the advice offered to me in response to a question about how to adopt better open science methods when posting to the arXiv:
For the sake of persistent archiving you should put all ancillary material at a sustainably archived website specifically designed to preserve scholarly communications material e.g. Zenodo https://zenodo.org/ or Dryad http://datadryad.org/ or Figshare https://figshare.com/
I agree with this advice entirely, and have in fact advocated this exact approach with both open-source efforts and reproducible papers. That said, let’s consider the incentive structure imposed by this approach. A student or postdoc taking responsibility for posting a reproducible work to the arXiv must then not only know how to do so directly, including how to write literate source code, but also about the existence of services such as Figshare. Moreover, a researcher must then manage their work’s presence on arXiv as well as additional services, increasing the complexity of maintaining an accessible research output.
Happily, however, arXiv itself supports including ancillary material such as source code and data along with a paper. Even here, though, the workflow for providing such ancillary material is more complicated than the comparable closed-science workflow. In particular, arXiv identifies ancillary material as being those files included in the anc/ subfolder of a submission package, but subfolders are only supported by uploading a ZIP archive of the entire submission. To make such a ZIP file with most existing tools, the original file must itself be in a folder called anc/, imposing a nontrivial technical restriction on project folder structures.
To some degree, encouragements of this kind that run counter to open science goals are inevitable. Indeed, there is a bit of a contradiction in that the very goal of reproducible research is to make it more difficult to publish in a way that is disporportionate between papers that are likely correct and those that cannot be as easily assessed for correctness. The natural tendency, then, is for reproducibility advocates to yell into the void or into the echo chamber about the existential importance of open science, and for the rest of the community to go forth with their business in the best way that they can given very limited resources.
In the same way as in dealing with discrimination by providing better tools that change incentive structures, we can break this circularity by providing better tools for writing reproducible papers. For instance, one very impressive tool to do precisely this is ReproZip, which works by leveraging modern software and hardware engineering technologies such as virtual machines. Indeed, ReproZip works great at making it easier to provide compact descriptions of reproducible research projects. This approach works especially well in combination with tools such as Jupyter Notebook, which allow for producing standardized and well-understood literate source code for a variety of different languages. Though Jupyter is perhaps most famous for its Python support, having grown out of the IPython project, it also supports Julia, R, F#, and even MATLAB when augmented with simple-to-install extensions.
Recently, I have started to experiment with other software tools for changing incentive structures, in the hopes of building on the backs of these efforts. My goals are of course more modest, in keeping with the resources available, but at the least I would like to propose ways of making tools such as Jupyter Notebook more accessible to arXiv users. In the rest of this post, I will detail two such (experimental!) efforts and how they are each motivated by reducing barriers to entry for reproducible physics research.
{revquantum}
The first such effort is the {revquantum} style file for LaTeX, intended to make it easier to write reproducible and accessible papers in the {revtex4-1} and {quantumarticle} document classes. The {revquantum} package supports accessiblility in a number of different ways:
-
Semantic notation: {revquantum} provides commands such as \newoperator, which allow users to write in a more semantic fashion than worrying about implementation details. In that example, \newoperator{Tr} defines \Tr as \newcommand{\Tr}{\operatorname{Tr}}, resulting in more readable code than what might be produced directly, such as \mathrm{Tr}(\rho).
-
Accessible color palettes: {revquantum} also provides definitions for the Color Universal Design palette, such that users can quickly set colors for TikZ diagrams and other features in an accessible manner.
-
{listings} integration: The {listings} package provides invaluable tools for including source code along with research manuscripts. There are some subtle issues in integrating {listings} with {revtex4-1} and other such classes, however, such that {revquantum} provides a reasonable set of defaults that for use with {revtex4-1}.
-
Package compatibility warnings: There are a few commonly-used packages which are known to be incompatible with {revtex4-1}. These incompatibilities can cause difficult-to-diagnose errors, however, instead of immediately raising errors that identify the problem. To address this and prevent users from being discouraged against modular TeX design, {revquantum} will raise warnings or errors when incompatible packages are loaded so that users are immediately informed as to the issue.
-
Bibliography improvements: The default BibTeX style file provided with {revtex4-1} suppresses the titles of cited papers in order to match the formatting that might appear in PRL and similar journals. For deployment to the arXiv, though, where space constraints are much less of an issue, this design decision removes context from the reader and encourages more of a focus on where something is published than the content that is being cited. To address this and encourage a stronger focus on research content, {revquantum} sets a default configuration that provides more context in generated bibliographies. Moreover, {revquantum} changes citation URLs to default to HTTPS, encouraging better security practices.
-
Annotations for collaborative writing: Finally, {revquantum} provides new lightweight commands such as \todo and \citeneed for annotating remaining tasks in a collaborative document. These commands leave warnings in the log file, making them easy to identify in modern text editors that annotate warnings in the TeX source. Moreover, the [final] option ot {revquantum} promotes these warnings to errors, providing a safety check against leaving outstanding tasks.
PoShTeX
The other effort I would like to detail a bit here is PoShTeX, a set of PowerShell tools for working with TeX-based research projects. In particular, PoShTeX provides the Export-ArXivArchive command, which makes a ZIP archive suitable for uploading to arXiv. In doing so, PoShTeX will rebuild the current TeX file, and will optionally re-run any nominated Jupyter Notebooks to ensure consistency with the figures and descriptions provided in the project’s main text. For example, a project might include a short Export-ArXiv.ps1 script to produce an arXiv-compatible archive:
#region Bootstrap PoShTeX
$modules = Get-Module -ListAvailable -Name posh-tex;
if (!$modules) {Install-Module posh-tex -Scope CurrentUser}
if (!($modules | ? {$_.Version -ge "0.1.4"})) {Update-Module posh-tex}
Import-Module posh-tex -Version "0.1.4"
#endregion
Export-ArXivArchive -RunNotebooks @{
ProjectName = "my-little-pauli";
TeXMain = "my-little-pauli.tex";
AdditionalFiles = @{
"fig/*.pdf" = "fig/";
"data/tomography-data.hdf5" = $null;
"revquantum.sty" = $null;
};
Notebooks = @(
"src/fidelity_is_magic.ipynb"
)
}
This script will then install PoShTeX if it is not already available, and will then rerun the listed notebooks, compile the TeX output, and produce the final build file my-little-pauli.zip for uploading to arXiv. In this way, PoShTeX makes it very straightforward to include reproducible material.
The second major functionality provided by PoShTeX is that it makes it much easier to write reusable LaTeX resources such as style files by making it easy to write installers and produce CTAN-compatible archives. This is, for example, how {revquantum} is packaged and uploaded to CTAN. Thus, PoShTeX hopefully also encourages not only sharing the research code itself but also the LaTeX code used to produce legible and readable research documents.
By the way, why PowerShell? It may seem like an odd choice for encouraging open scientific research, but consider that a very significant majority of Windows users already have PowerShell, given its status as a built-in tool since Windows 7. Though bash enjoys even wider deployment on macOS / OS X and on Linux, the [recent availability of PowerShell as an open source tool] on non-Windows platforms changes this calculus dramatically. In particular, given the ease of installing PowerShell modules with the Install-Module command, PowerShell may offer a way forward to distribute cross-platform shell libraries in an easy-to-use way.
In this post, I’ve described a few ways that what we encourage can have dramatic negative or hopefully positive effects on research culture and practice. These examples all speak to how thinking not only critically but also systematically can provide a path forward for doing the best science that we can.


